Hostname: page-component-cd9895bd7-p9bg8 Total loading time: 0 Render date: 2024-12-26T20:07:07.641Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiplicity Free Jacquet Modules

Published online by Cambridge University Press:  20 November 2018

Avraham Aizenbud  and
Dmitry Gourevitch
Avraham Aizenbud
Affiliation:
Massachussetts Institute of Technology, Cambridge, MA 02139, USAe-mail: [email protected]
Dmitry Gourevitch
Affiliation:
Faculty of Mathematics and Computer Science, The Weizmann Institute of Science, Rehovot 76100, Israele-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

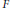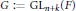Let $F$ be a non-Archimedean local field or a finite field. Let $n$ be a natural number and $k$ be 1 or 2. Consider $G\,:=\,\text{G}{{\text{L}}_{n+k}}\left( F \right)$ and let 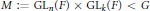$M\,:=\,\text{G}{{\text{L}}_{n}}\left( F \right)\,\times \,\text{G}{{\text{L}}_{k}}\left( F \right)\,<\,G$ be a maximal Levi subgroup. Let 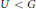$U\,<\,G$ be the corresponding unipotent subgroup and let 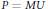$P\,=\,MU$ be the corresponding parabolic subgroup. Let 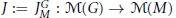$J\,:=\,J_{M}^{G}\,:\,\mathcal{M}\left( G \right)\,\to \,\mathcal{M}\left( M \right)$ be the Jacquet functor, i.e., the functor of coinvariants with respect to 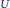$U$. In this paper we prove that 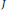$J$ is a multiplicity free functor, i.e.,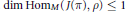$\dim\,\text{Ho}{{\text{m}}_{M}}\left( J\left( \pi \right),\,\rho \right)\,\le \,1$, for any irreducible representations $\pi $ of $G$ and $\rho $ of 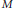$M$. We adapt the classical method of Gelfand and Kazhdan, which proves the “multiplicity free” property of certain representations to prove the “multiplicity free” property of certain functors. At the end we discuss whether other Jacquet functors are multiplicity free.

Keywords

20G0520C3020C3346F1047A67multiplicity oneGelfand pairinvariant distributionfinite group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 55 , Issue 4 , 01 December 2012 , pp. 673 - 688
Copyright
Copyright © Canadian Mathematical Society 2012

Footnotes

The authors were partially supported by a BSF grant, a GIF grant, and an ISF Center of excellency grant. The first author was also supported by ISF grant No. 583/09 and the second author by NSF grant DMS-0635607.

References

[1] Aizenbud, A., Avni, N., and Gourevitch, D., Spherical pairs over close local fields, Comment. Math. Helv., to appear. arxiv:0910.3199[math.RT].Google Scholar
[2] Aizenbud, A. and Gourevitch, D., Generalized Harish-Chandra descent, Gelfand pairs, and an Archimedean analog of Jacquet-Rallis’ heorem. Duke Math. J. 149(2009)no. 3, 509–567. http://dx.doi.org/10.1215/00127094-2009-044 Google Scholar
[3] Aizenbud, A. and Gourevitch, D., Multiplicity one theorem for (GLn+1(ℝ), GL n (ℝ)). Selecta Math. 15(2009), no. 2, 271–294. http://dx.doi.org/10.1007/s00029-009-0544-7 Google Scholar
[4] Aizenbud, A., Gourevitch, D., Rallis, S., and Schiffmann, G., Multiplicity one theorems. Ann. of Math. 172(2010), no. 2, 1407–1434.Google Scholar
[5] Bernstein, J., P-invariant distributions on GL(N) and the classification of unitary representations of GL(N) (non-archimedean case). In: Lie Group Representations, II. Lecture Notes in Math. 1041. Springer, Berlin, 1984, pp. 50–102.Google Scholar
[6] Bernstein, J., Representations of p-adic groups, lecture notes written by Karl E. Rumelhart at Harvard University, Fall 1992. Available at http://www.math.tau.ac.il/_bernstei/Publication_list/publication_texts/Bernst_Lecture_p-adic_repr.pdf.Google Scholar
[7] Bernstein, J. and Zelevinsky, A. V., Representations of the group GL(n, F), where F is a local non-Archimedean field. Uspekhi Mat. Nauk 10(1976), no. 3, 5–70.Google Scholar
[8] Deligne, P. La conjecture de Weil. II. Inst. Hautes études Sci. Publ. Math. 52(1980), 137–252.Google Scholar
[9] Faddeev, D. K., Complex representations of the general linear group over a finite field. Modules and representations. Zap. Nauchn. Sere. LOMI 46(1974), 64–88 (1974); English transl. J. Soviet Math. 9(1978), no. 3, 64–88.Google Scholar
[10] Gelfand, I. M. and Kazhdan, D., Representations of the group GL(n, K) where K is a local field. In: Lie Groups and Their Representations. Halsted, New York, 1975, pp. 95–118.Google Scholar
[11] Green, J. A., The characters of the finite general linear groups. Trans. Amer. Math. Soc. 80(1955), 402–447. http://dx.doi.org/10.1090/S0002-9947-1955-0072878-2 Google Scholar
[12] Goryachko, E. E., The simplicity of the branching of representations of the groups GL(n, q) under the parabolic restrictions. Zap. Nauchn. Semin. POMI 373(2009), 124–133; English transl. to appear in J. Math. Sci. (2010)Google Scholar
[13] Goryachko, E. E., An elementary proof of the simplicity of the branching of representations of the groups GL(n, q) under the parabolic restrictions. Funktsional. Anal. i Prilozhen 44(2010), no. 2, 82–87; English transl. Funct. Anal. Appl. 44(2010), no. 2, 146–150.Google Scholar
[14] Jacquet, H. and Rallis, S., Uniqueness of linear periods. Compositio Math. 102(1996), no. 1, 65–123.Google Scholar
[15] Sun, B. and Zhu, C.-B., Multiplicity one theorems: the archimedean case. Ann. of Math., to appear. arxiv:0903.1413[math.RT].Google Scholar
[16] Vershik, A. M. and Kerov, S. V., On an infinite-dimensional group over a finite field. Funktsional. Anal. i Prilozhen. 32(1998), no. 3, 3–10, 95; English transl. Funct. Anal. Appl. 32 (1998), no. 3, 147–152.Google Scholar
[17] Vershik, A. M. and Kerov, S. V., Four drafts on the representation theory of the group of infinite matrices over a finite field, preprint availiable at http://www.pdmi.ras.ru/znsl/2007/v344.html Google Scholar
[18] Zelevinsky, A. V.. Representations of Finite Classical Groups. A Hopf Algebra Approach. Lecture Notes in Mathematics 869. Springer-Verlag, Berlin, 1981.Google Scholar