Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-24T14:48:21.074Z Has data issue: false hasContentIssue false
  • English
  • Français

Multiple Scalar Transport

Published online by Cambridge University Press:  20 November 2018

Z. A. Melzak
Z. A. Melzak*
Affiliation:
University of British Columbia, Vancouver, British Columbia
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We shall consider scalar transport phenomena in which the mass distribution of a large number of interacting mass particles varies as a result of multiple coalescence mechanisms. Four models will be considered; all the particles are of the same kind in the first three. In the first model an integer n (n≥2) is given and the coalescence mechanism is such that under suitable conditions n particles of masses xl…, xn combine to form one particle of mass 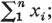we refer to this as the n/1 transport.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 16 , Issue 2 , June 1973 , pp. 257 - 268
Copyright
Copyright © Canadian Mathematical Society 1973

References

1. Drake, R. L., A general mathematical survey of the coagulation equation, National Center for Atmospheric Research, Boulder, Colorado, (mimeographed), 1971.Google Scholar
2. Goursat, E., Mathematical Analysis, Vol. 1, Ginn & Co., Boston, 1904.Google Scholar