Hostname: page-component-586b7cd67f-rdxmf Total loading time: 0 Render date: 2024-11-28T00:06:14.795Z Has data issue: false hasContentIssue false
  • English
  • Français

Monoidal Categories, 2-Traces, and Cyclic Cohomology

Part of: Higher algebraic $K$-theory Hopf algebras, quantum groups and related topics Categories with structure

Published online by Cambridge University Press:  07 January 2019

Mohammad Hassanzadeh ,
Masoud Khalkhali  and
Ilya Shapiro
Mohammad Hassanzadeh
Affiliation:
Department of Mathematics and Statistics, University of Windsor, Windsor, ON N9B 3P4 Email: [email protected]@uwindsor.ca
Masoud Khalkhali
Affiliation:
Department of Mathematics, The University of Western Ontario, London N6A 5B7, Ontario N6A 5B7 Email: [email protected]
Ilya Shapiro
Affiliation:
Department of Mathematics and Statistics, University of Windsor, Windsor, ON N9B 3P4 Email: [email protected]@uwindsor.ca
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we show that to a unital associative algebra object (resp. co-unital co-associative co-algebra object) of any abelian monoidal category (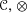$\mathscr{C},\otimes$) endowed with a symmetric 2-trace, i.e., an 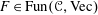$F\in \text{Fun}(\mathscr{C},\text{Vec})$ satisfying some natural trace-like conditions, one can attach a cyclic (resp. cocyclic) module, and therefore speak of the (co)cyclic homology of the (co)algebra “with coefficients in 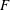$F$”. Furthermore, we observe that if 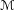$\mathscr{M}$ is a 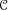$\mathscr{C}$-bimodule category and 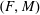$(F,M)$ is a stable central pair, i.e., 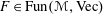$F\in \text{Fun}(\mathscr{M},\text{Vec})$ and 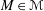$M\in \mathscr{M}$ satisfy certain conditions, then 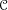$\mathscr{C}$ acquires a symmetric 2-trace. The dual notions of symmetric 2-contratraces and stable central contrapairs are derived as well. As an application we can recover all Hopf cyclic type (co)homology theories.

Keywords

monoidal categoryabelian and additive categorycyclic homologyHopf algebra

MSC classification

Primary: 16T05: Hopf algebras and their applications
Secondary: 18D10: Monoidal categories (= multiplicative categories), symmetric monoidal categories, braided categories 19D55: $K$-theory and homology; cyclic homology and cohomology
Type
Article
Information
Canadian Mathematical Bulletin , Volume 62 , Issue 2 , June 2019 , pp. 293 - 312
Copyright
© Canadian Mathematical Society 2018 

References

Bezrukavnikov, R., Finkelberg, M., and Ostrik, V., On tensor categories attached to cells in affine Weyl groups. III . Israel J. Math. 170(2009), 207–234. https://doi.org/10.1007/s11856-009-0026-9.Google Scholar
Bohm, G. and Stefan, D., A categorical approach to cyclic duality . J. Noncommut. Geom. 6(2012), no. 3, 481–538. https://doi.org/10.4171/JNCG/98.Google Scholar
Connes, A., Cohomologie cyclique et foncteurs Ext n . C. R. Acad. Sci. Paris Sér. I Math. 296(1983), no. 23, 953–958.Google Scholar
Connes, A. and Moscovici, H., Hopf algebras, cyclic cohomology and the transverse index theorem . Commun. Math. Phys. 198(1998), 199–246. https://doi.org/10.1007/s002200050477.Google Scholar
Connes, A. and Moscovici, H., Cyclic cohomology and Hopf algebras . Lett. Math. Phys. 48(1999), 97–108. https://doi.org/10.1023/A:1007527510226.Google Scholar
Dold, A. and Puppe, D., Duality, trace, and transfer . Proceedings of the Steklov Institute of Mathematics, 154(1984), 85–103.Google Scholar
Douglas, C. L., Schommer-Pries, C., and Snyder, N., Dualizable tensor categories. 2018. arxiv:1312.7188.Google Scholar
Etingof, P., Gelaki, S., Nikshych, D., and Ostrik, V., Tensor categories. Mathematical Surveys and Monographs, 205, American Mathematical Society, Providence, RI, 2015. https://doi.org/10.1090/surv/205.Google Scholar
Fuchs, J., Schaumann, G., and Schweigert, C., A trace for bimodule categories . Appl. Categ. Structures 25(2017), no. 2, 227–268. https://doi.org/10.1007/s10485-016-9425-3.Google Scholar
Hajac, P. M., Khalkhali, M., Rangipour, B., and Sommerhauser, Y., Hopf-cyclic homology and cohomology with coefficients . C. R. Math. Acad. Sci. Paris 338(2004), no. 9, 667–672. https://doi.org/10.1016/j.crma.2003.11.036.Google Scholar
Hajac, P. M., Khalkhali, M., Rangipour, B., and Sommerhauser, Y., Stable anti-Yetter–Drinfeld modules . C. R. Acad. Sci. Paris Ser. I 338(2004), 587–590. https://doi.org/10.1016/j.crma.2003.11.037.Google Scholar
Henriques, A., Penneys, D., and Tener, J., Categorified trace for module tensor categories over braided tensor categories . Doc. Math. 21(2016), 1089–1149.Google Scholar
Joyal, A., Street, R., and Verity, D., Traced monoidal categories . Math. Proc. Cambridge Philos. Soc. 119(1996), 447–468. https://doi.org/10.1017/S0305004100074338.Google Scholar
Kaledin, D., Cyclic homology with coefficients . In: Algebra, arithmetic, and geometry: in honor of Yu. I. Manin. Vol. II, Progr. Math., 270, Birkhäuser Boston, Inc., Boston, MA, 2009, pp. 23–47. https://doi.org/10.1007/978-0-8176-4747-6_2.Google Scholar
Kaledin, D., Trace theories and localization . In: Stacks and categories in geometry, topology, and algebra, Contemp. Math., 643, American Mathematical Society, Providence, RI, 2015, pp. 227–262. https://doi.org/10.1090/conm/643/12900.Google Scholar
Kassel, C., Quantum groups. Graduate Texts in Mathematics, 155, Springer-Verlag, New York, 1995. https://doi.org/10.1007/978-1-4612-0783-2.Google Scholar
Khalkhali, M. and Pourkia, A., Hopf cyclic cohomology in braided monoidal categories . Homology Homotopy Appl. 12(2010), no. 1, 111–155. https://doi.org/10.4310/HHA.2010.v12.n1.a9.Google Scholar
Kobyzev, I. and Shapiro, I., A categorical approach to cyclic cohomology of quasi-Hopf algebras and Hopf algebroids. 2018. arxiv:1803.09194.Google Scholar
Kobyzev, I. and Shapiro, I., Anti-Yetter–Drinfeld modules for quasi-Hopf algebras. arxiv:1804.02031. 2018.Google Scholar
Loday, J. L., Cyclic homology. Grundlehren der Mathematischen Wissenschaften, 301, Springer-Verlag, Berlin, 1992. https://doi.org/10.1007/978-3-662-21739-9.Google Scholar
Majid, S., Foundations of quantum group theory. Cambridge University Press, Cambridge, 1995. https://doi.org/10.1017/CBO9780511613104.Google Scholar
Majid, S., Quantum double for quasi-Hopf algebras . Lett. Math. Phys. 45(1998), no. 1, 1–9. https://doi.org/10.1023/A:1007450123281.Google Scholar
Ponto, K., Relative fixed point theory . Algebr. Geom. Topol. 11(2011), 839–886. https://doi.org/10.2140/agt.2011.11.839.Google Scholar
Ponto, K. and Shulman, M., Shadows and traces in bicategories . J. Homotopy Relat. Struct. 8(2013), 151–200. https://doi.org/10.1007/s40062-012-0017-0.Google Scholar
Schauenburg, P., Hopf modules and Yetter–Drinfel’d modules . J. Algebra 169(1994), 874–890. https://doi.org/10.1006/jabr.1994.1314.Google Scholar
Shapiro, I., Some invariance properties of cyclic cohomology with coefficients. 2016. arxiv:1611.01425.Google Scholar
Shapiro, I., On the anti-Yetter–Drinfeld module-contramodule correspondence. 2017. arxiv:1704.06552.Google Scholar
Yetter, D., Quantum groups and representations of monoidal categories . Math. Proc. Cambridge Philos. Soc. 108(1990), no. 2, 261–290. https://doi.org/10.1017/S0305004100069139.Google Scholar