Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-27T12:12:36.926Z Has data issue: false hasContentIssue false
  • English
  • Français

Moment Sequences and the Bernstein Polynomials*

Published online by Cambridge University Press:  20 November 2018

Sheldon M. Eisenberg
Sheldon M. Eisenberg*
Affiliation:
Lehigh University
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The Bernstein polynomials

(1.1)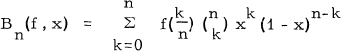

and the Bernstein power series

(1.2)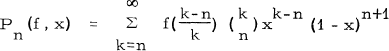

have been the subject of much research (e. g. [1; 2; 3; 6; 7; 8]). It is the purpose of this paper to demonstrate the relationship between these linear operators and certain classes of moment sequences defined below.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 4 , August 1969 , pp. 401 - 411
Copyright
Copyright © Canadian Mathematical Society 1969

Footnotes

*

This paper is a portion of the author's doctoral dissertation written at Lehigh University in 1967-68 under the direction of Professor J. P. King.

References

1. Arato, M. and Renyi, A., Probabilistic proof of a theorem on the approximation of continuous functions by means of generalized Bernstein polynomials. Acta. Math. Acad. Sci. Hungar. 8 (1957) 91–97.Google Scholar
2. Boehme, T.K. and Powell, R. E., Positive linear operators generated by analytic functions. SIAM J. Appl. Math. 16 (1968) 510–519.Google Scholar
3. Cheney, E. W. and Sharma, A., Bernstein power series. Canad. J. Math. 16 (1964) 241–252.Google Scholar
4. Hardy, G. H., Divergent series. (Oxford at the Clarendon Press, London, 1949.)Google Scholar
5. Korovkin, P., Linear operators and approximation theory. (Translated from the Russian edition of 1959) (Delhi, 1960.)Google Scholar
6. Lorentz, G.G., Bernstein polynomials. (Mathematical Expositions, No. 8, University of Toronto Press, Toronto, 1953.)Google Scholar
7. Meyer-König, W. and Zeller, K., Bernsteinsche potenzreihen. Stud. Math. 19 (1960) 89–94.Google Scholar
8. Wood, B., On a generalized Bernstein polynomial of Jakimovski and Leviatan. Math. Zeitschr. 106 (1968) 170–174.Google Scholar