Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-30T20:47:47.724Z Has data issue: false hasContentIssue false
  • English
  • Français

Moment Problems and Quasi-Hausdorff Transformations

Published online by Cambridge University Press:  20 November 2018

Dany Leviatan
Dany Leviatan*
Affiliation:
University of Illinois, Urbana
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The sequence to sequence quasi - Hausdorff transformations were defined by Hardy [1] 1 1. 19 p. 277 as follows. For a given sequence {μn} (n ≥ 0) of real or complex numbers, define the operator Δ by 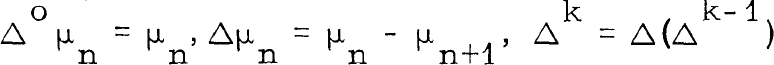for k > l. {tm} (m ≥ 0) is called the sequence to sequence quasi-Hausdorff transform by means of {μn} (or, in short, the [QH, μn] transform) of {sn} (n ≥ 0) if if 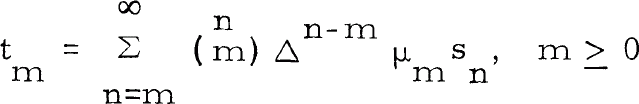, provided that the sums on the right-hand side converge for all m ≥ 0. Ramanujan in [11] and [12] has defined the series to series quasi-Hausdorff transformation s and has proved necessary and sufficient conditions for the regularity of the two kinds of transformations.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 11 , Issue 2 , June 1968 , pp. 225 - 236
Copyright
Copyright © Canadian Mathematical Society 1968

References

1. Hardy, G.H., Divergent series. (Oxford, 1949).Google Scholar
2. Hausdorff, F., Summationsmethoden und momentenfolgen II. Math. Z. 9 (1921) 280-299.Google Scholar
3. Jakimovski, A., The product of summability methods; new classes of transformations and their properties. Technical (scientific) note no.4, contract no. AF 61 (052)-187, (1959).Google Scholar
4. Jakimovski, A. and Leviatan, D., A property of approximation operators and applications to Tauberian constants. Math. Z. 102, (1967) 177-204.,Google Scholar
5. Jakimovski, A., Completeness and approximation operators. J. Indian Math. Soc. (to appear).Google Scholar
6. Jakimovski, A. and Ramanujan, M.S., A uniform approximation theorem and its application to moment problems. Math. Z. 84 (1964) 143-153.Google Scholar
7. Krasnosel'skii, M.A. and Rutickii, Ya. B., Convex functions and Orlicz spaces. (Translated by Boron, Leo F.). (Noordhoff, P. Ltd.- Groningen the Netherlands, 1961).Google Scholar
8. Leviatan, D., A generalized moment problem. Israel J. Math. 5 (1967) 97-103. Google Scholar
9. Leviatan, D., Some moment problems in a finite interva l. Canadian J. Math, (to appear).Google Scholar
10. Lorentz, G.G., Bernstein polynomials. (Toronto Univ. Press, 1953).Google Scholar
11. Ramanujan, M.S., Series to series quasi-Hausdorff transformations. J. Indian Math. Soc. 17 (1953)47-53.Google Scholar
12. Ramanujan, M.S., On Hausdorff and quasi-Hausdorff methods of summability. Quart. J. Math. (Oxford second series) 8 (1957) 197-213.Google Scholar
13. Ramanujan, M.S., The moment problem in a certain function space of G.G. Lorentz. Archiv der Math. 15 (1964) 71-75.Google Scholar
14. Zygmund, A., Trigonometric series I, second edition. Cambridge Univ. Press.Google Scholar