Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-25T17:56:02.855Z Has data issue: false hasContentIssue false
  • English
  • Français

Moduli Spaces of Metrics of Positive Scalar Curvature on Topological Spherical Space Forms

Part of: Global differential geometry

Published online by Cambridge University Press:  24 February 2020

Philipp Reiser
Philipp Reiser*
Affiliation:
Institut für Mathematik, Karlsruher Institut für Technologie (KIT)Germany Email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 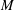$M$ be a topological spherical space form, i.e., a smooth manifold whose universal cover is a homotopy sphere. We determine the number of path components of the space and moduli space of Riemannian metrics with positive scalar curvature on 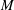$M$ if the dimension of 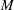$M$ is at least 5 and 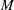$M$ is not simply-connected.

Keywords

moduli spacetopological spherical space formpositive scalar curvature

MSC classification

Primary: 53C20: Global Riemannian geometry, including pinching
Type
Article
Information
Canadian Mathematical Bulletin , Volume 63 , Issue 4 , December 2020 , pp. 901 - 908
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

References

Bamler, R. H. and Kleiner, B., Ricci flow and contractibility of spaces of metrics. 2019. arxiv:1909.08710Google Scholar
Botvinnik, B. and Gilkey, P. B., The eta invariant and metrics of positive scalar curvature. Math. Ann. 302(1995), 507–517. https://doi.org/10.1007/BF01444505CrossRefGoogle Scholar
Botvinnik, B. and Gilkey, P. B., Metrics of positive scalar curvature on spherical space forms. Canad. J. Math. 48(1996), 64–80. https://doi.org/10.4153/CJM-1996-003-0CrossRefGoogle Scholar
Cartan, H. and Eilenberg, S., Homological algebra. Princeton University Press, Princeton, NJ, 1956.Google Scholar
Dinkelbach, J. and Leeb, B., Equivariant Ricci flow with surgery and applications to finite group actions on geometric 3-manifolds. Geom. Topol. 13(2009), 1129–1173. https://doi.org/10.2140/gt.2009.13.1129CrossRefGoogle Scholar
Franc, A., Spin structures and Killing spinors on lens spaces. J. Geom. Phys. 4(1987), 277–287. https://doi.org/10.1016/0393-0440(87)90015-5CrossRefGoogle Scholar
Hambleton, I., Topological spherical space forms. 2014. arxiv:1412.8187Google Scholar
Karoubi, M., Algèbres de Clifford et K-théorie. Ann. Sci. École Norm. Sup. 1(1968), 161–270.CrossRefGoogle Scholar
Kwasik, S. and Schultz, R., Positive scalar curvature and periodic fundamental groups. Comment. Math. Helv. 65(1990), 271–286. https://doi.org/10.1007/BF02566607CrossRefGoogle Scholar
Kwasik, S. and Schultz, R., Fake spherical spaceforms of constant positive scalar curvature. Comment. Math. Helv. 71(1996), 1–40. https://doi.org/10.1007/BF02566407CrossRefGoogle Scholar
Blaine Lawson, H. Jr. and Michelsohn, M.-L., Spin geometry. Princeton Mathematical Series, 38, Princeton University Press, Princeton, NJ, 1989.Google Scholar
López de Medrano, S., Involutions on manifolds. Ergebnisse der Mathematik und ihrer Grenzgebiete, 59, Springer-Verlag, New York, Heidelberg, 1971.CrossRefGoogle Scholar
Marques, F. C., Deforming three-manifolds with positive scalar curvature. Ann. of Math. (2) 176(2012), 815–863. https://doi.org/10.4007/annals.2012.176.2.3CrossRefGoogle Scholar
Morgan, J. and Tian, G., The geometrization conjecture. Clay Mathematics Monographs, 5, American Mathematical Society, Providence, RI; Clay Mathematics Institute, Cambridge, MA, 2014.Google Scholar
Rosenberg, J. and Stolz, S., Metrics of positive scalar curvature and connections with surgery. In: Surveys on surgery theory, Vol. 2. Ann. of Math. Stud., 149, Princeton Univ. Press, Princeton, NJ, 2001, pp. 353–386.Google Scholar
Stolz, S., Simply connected manifolds of positive scalar curvature. Ann. of Math. (2) 136(1992), 511–540. https://doi.org/10.2307/2946598CrossRefGoogle Scholar
Tuschmann, W., Spaces and moduli spaces of Riemannian metrics. Front. Math. China 11(2016), 1335–1343. https://doi.org/10.1007/s11464-016-0576-1CrossRefGoogle Scholar
Tuschmann, W. and Wraith, D. J., Moduli spaces of Riemannian metrics. Second corrected printing, Oberwolfach Seminars, 46, Birkhäuser Verlag, Basel, 2015. https://doi.org/10.1007/978-3-0348-0948-1CrossRefGoogle Scholar
Wall, C. T. C., Surgery on compact manifolds, Second ed., Mathematical Surveys and Monographs, 69, American Mathematical Society, Providence, RI, 1999. https://doi.org/10.1090/surv/069CrossRefGoogle Scholar
Wolf, J. A., Spaces of constant curvature. McGraw-Hill Book Co., New York, London, Sydney, 1967.Google Scholar