Hostname: page-component-586b7cd67f-tf8b9 Total loading time: 0 Render date: 2024-11-24T10:49:12.386Z Has data issue: false hasContentIssue false
  • English
  • Français

Modules Et Anneaux Quasi-Continus

Published online by Cambridge University Press:  20 November 2018

Louis Jeremy
Louis Jeremy*
Affiliation:
Département De Mathématiques, Université De Poitiers 40, Avenue Du Recteur Pineau 86—Poitiers France, France
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Le but de ce travail est de prolonger les travaux de Y. Utumi sur les anneaux continus.

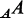Nous appelons module quasi-continu un module stable par tout projecteur de son enveloppe injective. Un anneau unitaire A est dit quasi-continu à gauche (resp. à droite) si le A-module à gauche (resp. à droite 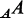) est quasi-continu. Cette définition est plus générale que celle d'anneau continu à gauche donnée par Yuzo Utumi, et quand l'anneau est régulier, elles coïncident (§111).

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 17 , Issue 2 , 01 June 1974 , pp. 217 - 228
Copyright
Copyright © Canadian Mathematical Society 1974

References

1. Bichot, J., Essentialité et importance dans les modules (Doctorat de spécialité Faculté des Sciences de Lyon, 20 septembre 1968. Imprimé à Beyrouth, 1969).Google Scholar
2. Cailleau, A. et Renault, G., Etude des modules ∑-quasi-injectifs. C.R. Acad. Se. Paris, t. 270, p. 1391-1394 (1er juin 1970).Google Scholar
3. Cailleau, A. et Renault, G., Anneau associé à une somme directe infinie de modules quasi-injectifs. Archiv. der Mathematik, vol. XXI, 1970 fasc. 6 (p. 561-566).Google Scholar
4. Faith, C., Rings with ascending condition on annihilators. Nagoya Math. J. 27–1 (1966), p. 179–191.Google Scholar
5. Fuchs, L., Abelian groups. Pergamon Press, 1960.Google Scholar
6. Kaplansky, L., Rings of operators. W. A. Benjamin, Inc., 1968.Google Scholar
7. Lambek, J., Lectures on rings and modules (Blaisdell Publishing Company) 1966.Google Scholar
8. Osofsky, B., Endomorphism rings of quasi-injective modules. Can. J. Math. Vol. 20, n∘ 4 (1968), p. 895-903.Google Scholar
9. Renault, G., Thèse Bull. Soc. Math. France, mémoire 9, supplément au numéro de mars 1967.Google Scholar
10. Renault, G., Anneaux réduits non commutatifs. Journal de Mathématiques pures et appliquées 46, 1967, p. 203-214.Google Scholar
11. Renault, G., Anneau associé à un module injectif. Bull. Soc. Math. 2 ème série, 92, 1968, p. 53-58.Google Scholar
12. Utumi, Y., On continuous regular rings and semi-simple self-injective rings. Can. J. Math. 12 (1960), p. 597-605.Google Scholar
13. Utumi, Y., On continuous regular rings. Can. Math. Bull. 4 (1961), p. 63-69.Google Scholar
14. Utumi, Y., On rings of which any one sided quotient rings are two-sided. Proc. Amer. Math. Soc, 14, (1963), p. 141-147.Google Scholar
15. Utumi, Y., On continuous rings and self-injective rings, Trans. Amer. Math. Soc. 118 (1965), p. 158-173.Google Scholar
16. Wofson, K. G., An ideal theoretic characterization of the ring of all linear transformations, Amer. J. Math., 75 (1957), 358-386.Google Scholar
17. Zelinsky, D., Every linear transformation is a sum of non-singular ones, Proc. Amer. Math. Soc, 5 (1954), 627-630.Google Scholar