Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-20T10:42:26.887Z Has data issue: false hasContentIssue false
  • English
  • Français

Modular Reduction in Abstract Polytopes

Published online by Cambridge University Press:  20 November 2018

B. Monson  and
Egon Schulte
B. Monson
Affiliation:
University of New Brunswick, Fredericton, NB E3B 5A3 e-mail: [email protected]
Egon Schulte
Affiliation:
Northeastern University, Boston, MA, U.S.A. 02115 e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The paper studies modular reduction techniques for abstract regular and chiral polytopes, with two purposes in mind: first, to survey the literature about modular reduction in polytopes; and second, to apply modular reduction, with moduli given by primes in 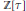$\mathbb{Z}\left[ \tau \right]$ (with $\tau$ the golden ratio), to construct new regular 4-polytopes of hyperbolic types 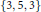$\{3,\,5,\,3\}$ and 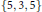$\{5,\,3,\,5\}$ with automorphism groups given by finite orthogonal groups.

Keywords

51M2020F55abstract polytopesregular and chiralCoxeter groupsmodular reduction
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 3 , 01 September 2009 , pp. 435 - 450
Copyright
Copyright © Canadian Mathematical Society 2009

References

[1] Artin, E., Geometric Algebra. Interscience, New York, 1957.Google Scholar
[2] Bisztriczky, T., McMullen, P., Schneider, R., and Weiss, A. I., (eds.), Polytopes: Abstract, Convex and Computational. NATO ASI Series C 440. Kluwer, Dordrecht, 1994.Google Scholar
[3] Chen, L., Moody, R., and Patera, J., Non-crystallographic root systems. In: Quasicrystals and Discrete Geometry. Fields Inst. Monogr. 10, American Mathematical Society, Providence, RI, 1998, pp. 135–178.Google Scholar
[4] Conder, M., Hubard, I., and Pisanski, T., Constructions for chiral polytope. J. London Math. Soc. 77(2008), no. 1, 115–129.Google Scholar
[5] Coxeter, H. S. M., Extreme forms. Canad. J. Math. 3(1951), 391–441.Google Scholar
[6] Coxeter, H. S. M., Ten toroids and fifty-seven hemidodecahedr. Geom. Dedicata 13(1982), 87–99.Google Scholar
[7] Coxeter, H. S. M., A symmetrical arrangement of eleven hemi-icosahedra. In: Convexity and Graph Theory. North-Holland Math. Stud. 87. North-Holland, Amsterdam, 1984, pp. 391–441.Google Scholar
[8] Coxeter, H. S. M. and Moser, W. O. J., Generators and Relations for Discrete Groups. Third edition. Springer-Verlag, New York, 1972.Google Scholar
[9] Curtis, C. W. and Reiner, I., Representation Theory of Finite Groups and Associative Algebras. Interscience, New York, 1962.Google Scholar
[10] Dodd, F. W., Number Theory in the Quadratic Field with Golden Section Unit. Examples of Mathematical Structures 3, Polygonal Publishing House, Passaic, NJ, 1983.Google Scholar
[11] Grünbaum, B., Regularity of graphs, complexes and designs. In: Problèmes combinatoires et théorie des graphes, Colloq. Internat. CNRS 260, Paris, 1978, pp. 191–197.Google Scholar
[12] Hartley, M. I. and Leemans, D., Quotients of a universal locally projective polytope of type ﹛5, 3, 5﹜ . Math. Zeit. 247(2004), no. 4, 663–674.Google Scholar
[13] Hartley, M. I. and Leemans, D., On locally spherical polytopes of type ﹛5, 3, 5﹜ . Discrete Math. 309(2009), no. 1, 247–254.Google Scholar
[14] Humphries, J. E., Reflection Groups and Coxeter Groups. Cambridge University Press, Cambridge, 1990.Google Scholar
[15] Jones, G. A. and Long, C. D., Epimorphic images of the [5, 3, 5] Coxeter group. To appear in Math. Z.Google Scholar
[16] Kantor, W., Generation of linear groups. In: The Geometric Vein. Springer, New York, 1981, pp. 497–509.Google Scholar
[17] Leemans, D. and Schulte, E., Groups of type L 2(q) acting on polytopes. Adv. Geom. 7(2007), no. 4, 529–539.Google Scholar
[18] McMullen, P., Regular polyhedra related to projective linear groups. Discrete Math. 91(1991), 161–170.Google Scholar
[19] McMullen, P., Monson, B. R. and Weiss, A. I., Regular maps constructed from linear groups. European J. Combin. 14(1993), 541–552.Google Scholar
[20] McMullen, P. and Schulte, E., Abstract Regular Polytopes. Encyclopedia of Mathematics and Its Applications 92. Cambridge University Press, Cambridge, 2002.Google Scholar
[21] Monson, B., Simplicial quadratic forms. Canad. J. Math. 35(1983), 101–116.Google Scholar
[22] Monson, B. and Schulte, E., Reflection groups and polytopes over finite fields. I. Adv. in Appl.Math. 33(2004), no. 2, 290–317.Google Scholar
[23] Monson, B. and Schulte, E., Reflection groups and polytopes over finite fields. II. Adv. in Appl. Math. 38(2007), no. 3, 327–356.Google Scholar
[24] Monson, B. and Schulte, E., Reflection groups and polytopes over finite fields. III. Adv. in Appl. Math. 41(2008), no. 1, 76–94.Google Scholar
[25] Monson, B. and Schulte, E., Locally toroidal polytopes and modular linear groups. To appear in Discrete Math.Google Scholar
[26] Monson, B. and Weiss, A. I., Regular 4-polytopes related to general orthogonal groups. Mathematika 37(1990), 106–118.Google Scholar
[27] Monson, B. and Weiss, A. I., Polytopes related to the Picard group. Linear Algebra Appl. 218(1995), 185–204.Google Scholar
[28] Monson, B. and Weiss, A. I., Eisenstein integers and related C-groups. Geom. Dedicata 66(1997), no. 1, 99–117.Google Scholar
[29] Nostrand, B. and Schulte, E., Chiral polytopes from hyperbolic honeycombs. Discrete Comput. Geom. 13(1995), no. 1, 17–39.Google Scholar
[30] Schulte, E. and Weiss, A. I., Chirality and projective linear groups. Discrete. Math. 131(1994), no. 1-3, 221–261.Google Scholar
[31] Wagner, A., Determination of the finite primitive reflection groups over an arbitrary field of characteristic not two. I. Geom. Dedicata 9(1980), no. 2, 239–253.Google Scholar
[32] Wagner, A., Determination of the finite primitive reflection groups over an arbitrary field of characteristic not two. II, III. Geom. Dedicata 10(1981), no. 1-4, 191–203, 475–523.Google Scholar
[33] Weiss, A. I., Incidence polytopes with toroidal cells. Discrete Comput. Geom. 4(1989), no. 1, 55–73.Google Scholar
[34] Wilson, S. E., Applications and refinements of Vince's construction. Geom. Dedicata 48(1993), no. 2, 231–242.Google Scholar
[35] Zalesskiĭ, A. E. and Serežkin, V. N., Linear groups generated by transvections. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 40(1976), 26–49. (English translation inMath. USSR Izvestija 10(1976), 25–46.)Google Scholar
[36] Zalesskiĭ, A. E. and Serežkin, V. N., Finite linear groups generated by reflections. (Russian) Izv. Akad. Nauk SSSR Ser. Mat. 44(1980), 1279–1307, 38. (English translation inMath. USSR Izvestija 17(1981), 477–503.)Google Scholar