Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Bacsich, P. D.
1973.
Primality and model-completions.
Algebra Universalis,
Vol. 3,
Issue. 1,
p.
265.
Volger, Hugo
1979.
Preservation theorems for limits of structures and global sections of sheaves of structures.
Mathematische Zeitschrift,
Vol. 166,
Issue. 1,
p.
27.
Makkai, M.
1987.
Stone duality for first order logic.
Advances in Mathematics,
Vol. 65,
Issue. 2,
p.
97.
Volger, Hugo
1988.
CSL '87.
Vol. 329,
Issue. ,
p.
322.
Moraschini, T.
and
Wannenburg, J.J.
2020.
Epimorphism surjectivity in varieties of Heyting algebras.
Annals of Pure and Applied Logic,
Vol. 171,
Issue. 9,
p.
102824.
Moraschini, T.
Raftery, J. G.
and
Wannenburg, J. J.
2020.
Epimorphisms, Definability and Cardinalities.
Studia Logica,
Vol. 108,
Issue. 2,
p.
255.


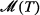 be the category of models of
be the category of models of 