Hostname: page-component-cd9895bd7-jkksz Total loading time: 0 Render date: 2024-12-27T11:20:35.150Z Has data issue: false hasContentIssue false
  • English
  • Français

Mixed Norm Decay for the Klein-Gordon Equation with Initial Data in Lp

Published online by Cambridge University Press:  20 November 2018

Bernard Marshall
Bernard Marshall*
Affiliation:
McGill University, Montréal, Québec
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper gives necessary conditions for mixed norm estimates from Lp to Lr (Lq) for solutions of the Klein-Gordon equation

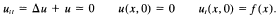
These conditions are best possible if p = 2 or

Keywords

35L15
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 29 , Issue 1 , 01 March 1986 , pp. 11 - 19
Copyright
Copyright © Canadian Mathematical Society 1986

References

1. Brenner, P., On space-time means and everywhere defined scattering operators for nonlinear Klein- Gordon equations, preprint.Google Scholar
2. Marshall, B., Strauss, W., and Wainger, S., Lp-Lq estimates for the Klein-Gordon equation, J. Math. Pures et Appl. 59 (1980), pp. 417–440.Google Scholar
3. Marshall, B., Mixed norm estimates for the Klein-Gordon equation, Proceedings of Conference in Harmonic Analysis for A. Zygmund, part 2, (1982), pp. 614–625.Google Scholar
4. Pécher, H., Nonlinear small data scattering for the wave and Klein-Gordon equation, preprint.Google Scholar
5. Strauss, W. A., Nonlinear scattering theory at low energy, I.J. Funct. Anal. 41 (1981), pp. 110— 113. II, ibid. 43(1981), pp. 281–293.Google Scholar
6. Strichartz, R. S., Restrictions of Fourier transforms to quadratic surfaces and decay of solutions of wave equations, Duke Math. J. 44 (1977), pp. 705–714.Google Scholar