Hostname: page-component-6bf8c574d5-2jptb Total loading time: 0 Render date: 2025-02-17T15:21:47.322Z Has data issue: false hasContentIssue false
  • English
  • Français

Minimal Non Self Dual Groups

Published online by Cambridge University Press:  20 November 2018

Lili Li  and
Guiyun Chen
Lili Li
Affiliation:
School of Mathematics and Computation Science, Lingnan Normal University, Zhanjiang, China e-mail: [email protected]
Guiyun Chen
Affiliation:
(Corr. Author) School of Mathematics and Statistics, Southwest University, Chongqing, China e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

A group 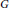$G$ is self dual if every subgroup of 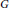$G$ is isomorphic to a quotient of 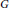$G$ and every quotient of 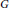$G$ is isomorphic to a subgroup of 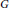$G$. It is minimal non self dual if every proper subgroup of 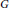$G$ is self dual but 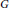$G$ is not self dual. In this paper, the structure of minimal non self dual groups is determined.

Keywords

20D15minimal non self dual groupfinite groupmetacyclic groupmetabelian group
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 538 - 547
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] An, L. J., Ding, J. R., and Zhang, Q. H., Finite self dual groups. J. Algebra 341(2011), 35–44. http://dx.doi.Org/1 0.101 6/j.jalgebra.2O11.06.014 Google Scholar
[2] Holder, O., Die Gruppen der Ordnungen p^.pq2, pqr, p4. Math.Annal. 43(1893), 301–412. http://dx.doi.org/10.1007/BF01443651 Google Scholar
[3] Huppert, B., EndlicheGruppen I. Grundlehren Math. Wiss.134, Springer-Verlag, 1967.Google Scholar
[4] Iwasawa, K., Ùberdie endlichenGruppen und die VerbandeihrerUntergruppen. J. Fac. Sci. Imp. Univ. Tokyo Sect. I. 4(1941), 171–199.Google Scholar
[5] Rédei, L., Das schiefe Product in der Gruppentheorie. Comment.Math.Helv. 20(1947), 225–264. http://dx.doi.org/10.1007/BF02568131 Google Scholar
[6] Spencer, A. E., Self dual finite groups. 1st. Veneto Sci. Lett.ArtiAtti Cl. Sci. Mat.Natur. 130(1971/72), 385–391.Google Scholar
[7] Xu, M. Y., An, L. J., and Zhang, Q. H., Finite p-groups all of whose nonabelian proper subgroups are generated by two elements. J. Algebra. 319(2008), 3603–3620. http://dx.doi.Org/1 0.101 6/j.jalgebra.2008.01.045 Google Scholar
[8] Xu, M. Y., A theorem on metabelian p-groups and some consequences. Chinese Ann. Math. Ser. B 5(1984), 1–6.Google Scholar
[9] Zhang, Q. H., Sun, X. J., An, L. J., and Xu, M. Y., Finite p-groups all of whose subgroups of index p2 areabelian. Algebra Colloq. 15(2008), 167–180. http://dx.doi.org/! 0.1142/S10053867080001 63 Google Scholar