Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-27T09:12:00.344Z Has data issue: false hasContentIssue false
  • English
  • Français

Metrizability of Holonomy Invariant Projective Deformation of Sprays

Part of: Variational problems in infinite-dimensional spaces Local differential geometry Global differential geometry Infinite-dimensional manifolds Miscellaneous topics in calculus of variations and optimal control

Published online by Cambridge University Press:  23 January 2020

S. G. Elgendi  and
Zoltán Muzsnay
S. G. Elgendi
Affiliation:
Department of Mathematics, Faculty of Science, Benha University, Egypt e-mail: [email protected]
Zoltán Muzsnay
Affiliation:
Institute of Mathematics, University of Debrecen, Debrecen, Hungary e-mail: [email protected] URL: http://math.unideb.hu/muzsnay-zoltan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we consider projective deformation of the geodesic system of Finsler spaces by holonomy invariant functions. Starting with a Finsler spray 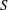$S$ and a holonomy invariant function 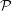${\mathcal{P}}$, we investigate the metrizability property of the projective deformation 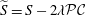$\widetilde{S}=S-2\unicode[STIX]{x1D706}{\mathcal{P}}{\mathcal{C}}$. We prove that for any holonomy invariant nontrivial function 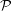${\mathcal{P}}$ and for almost every value 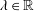$\unicode[STIX]{x1D706}\in \mathbb{R}$, such deformation is not Finsler metrizable. We identify the cases where such deformation can lead to a metrizable spray. In these cases, the holonomy invariant function 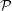${\mathcal{P}}$ is necessarily one of the principal curvatures of the geodesic structure.

Keywords

sprayprojective deformationmetrizability problemholonomy invariant functionholonomy distribution

MSC classification

Primary: 53C60: Finsler spaces and generalizations (areal metrics)
Secondary: 53B40: Finsler spaces and generalizations (areal metrics) 58B20: Riemannian, Finsler and other geometric structures 49N45: Inverse problems 58E30: Variational principles
Type
Article
Information
Canadian Mathematical Bulletin , Volume 66 , Issue 3 , September 2023 , pp. 701 - 714
Check for updates
Copyright
© Canadian Mathematical Society 2020

Footnotes

This work is partially supported by the EFOP-3.6.2-16-2017-00015 and EFOP-3.6.1-16-2016-00022 projects and the 307818 TKA-DAAD exchange project.

References

Alvarez Paiva, J. C., Symplectic geometry and Hilbert’s fourth problem . J. Differential Geometry 69(2005), 353–378.Google Scholar
Bucataru, I. and Dahl, M. F., Semi basic 1-forms and Helmholtz conditions for the inverse problem of the calculus of variations . J. Geom. Mech. 1(2009), 159–180. https://doi.org/10.3934/jgm.2009.1.159 Google Scholar
Bucataru, I. and Muzsnay, Z., Projective and Finsler metrizability: parameterization-rigidity of the geodesics . Int. J. Math. 23(2012), no. 9, 1250099. https://doi.org/10.1142/S0129167X12500991 Google Scholar
Bucataru, I. and Muzsnay, Z., Projective metrizability and formal integrability . SIGMA Symmetry Integrability Geom. Methods Appl. 7(2011), Paper 114. https://doi.org/10.3842/SIGMA.2011.114 Google Scholar
Chern, S. S. and Shen, Z., Riemann–Finsler geometry . Nankai Tracts in Mathematics, 6, World Scientific Publishers, Hackensack, NJ, 2005. https://doi.org/10.1142/5263 CrossRefGoogle Scholar
Crampin, M., On the inverse problem for sprays . Publ. Math. Debrecen 70(2007), 319–335.CrossRefGoogle Scholar
Eastwood, M. and Matveev, V. S., Metric connections in projective differential geometry . In: Symmetries and overdetermined systems of partial differential equations . IMA Vol. Math. Appl., 144, Springer, New York, 2008, pp. 339–350. https://doi.org/10.1007/978-0-387-73831-4_16 CrossRefGoogle Scholar
Grifone, J., Structure presque-tangente et connexions. I . Ann. Inst. Fourier (Grenoble) 22(1972), 287–334.CrossRefGoogle Scholar
Grifone, J. and Muzsnay, Z., Variational principles for second order differential equations. Application of the Spencer theory to characterize variational sprays . World Scientific, River Edge, NJ, 2000. https://doi.org/10.1142/9789812813596 CrossRefGoogle Scholar
Krupka, D. and Sattarov, A. E., The inverse problem of the calculus of variations for Finsler structures . Math. Slovaca 35(1985), 217–222.Google Scholar
Krupková, O., Variational metric structures . Publ. Math. Debrecen 62(2003), no. 3–4, 461–495.CrossRefGoogle Scholar
Muzsnay, Z., The Euler–Lagrange PDE and Finsler metrizability . Houston J. Math. 32(2006), 79–98.Google Scholar
Shen, Z., Differential geometry of spray and Finsler spaces . Kluwer Academic Publishers, Dordrecht, 2001. https://doi.org/10.1007/978-94-015-9727-2 CrossRefGoogle Scholar
Shen, Z., Geometric meanings of curvatures in Finsler geometry . Proceedings of the 20th Winter School “Geometry and Physics” Rend. Circ. Mat. Palermo (2) 66(2001), Suppl., 165–178.Google Scholar
Szilasi, J. and Vattamany, S., On the Finsler-metrizabilities of spray manifolds . Period. Math. Hungar. 44(2002), 81–100. https://doi.org/10.1023/A:1014928103275 CrossRefGoogle Scholar
Yang, G., Some classes of sprays in projective spray geometry . Diff. Geom. Appl. 29(2011), 606–614. https://doi.org/10.1016/j.difgeo.2011.04.041 CrossRefGoogle Scholar