Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Sadybekov, Makhmud
and
Derbissaly, Bauyrzhan
2021.
On Green’s function of Cauchy–Dirichlet problem for hyperbolic equation in a quarter plane.
Boundary Value Problems,
Vol. 2021,
Issue. 1,


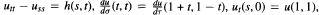 for
for 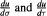 represent the directional derivatives of
represent the directional derivatives of 