Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-24T19:08:21.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Measurements and Gδ-Subsets of Domains

Published online by Cambridge University Press:  20 November 2018

Harold Bennett  and
David Lutzer
Harold Bennett
Affiliation:
Mathematics Department, Texas Tech University, Lubbock, TX, 79409e-mail: [email protected]
David Lutzer
Affiliation:
Mathematics Department, College of William and Mary, Williamsburg, VA, 23187e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper we study domains, Scott domains, and the existence of measurements. We use a space created by D. K. Burke to show that there is a Scott domain $P$ for which 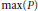$\max (P)$ is a 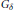${{G}_{\delta }}$-subset of $P$ and yet no measurement $\mu $ on $P$ has 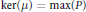$\text{ker(}\mu \text{)}\,=\,\max (P)$. We also correct a mistake in the literature asserting that 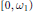$[0,\,{{\omega }_{1}})$ is a space of this type. We show that if $P$ is a Scott domain and 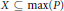$X\,\subseteq \,\max (P)$ is a 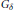${{G}_{\delta }}$-subset of $P$, then 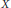$X$ has a 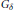${{G}_{\delta }}$-diagonal and is weakly developable. We show that if 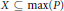$X\,\subseteq \,\max (P)$ is a 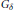${{G}_{\delta }}$-subset of $P$, where $P$ is a domain but perhaps not a Scott domain, then 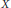$X$ is domain-representable, first-countable, and is the union of dense, completely metrizable subspaces. We also show that there is a domain $P$ such that 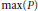$\max (P)$ is the usual space of countable ordinals and is a 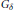${{G}_{\delta }}$-subset of $P$ in the Scott topology. Finally we show that the kernel of a measurement on a Scott domain can consistently be a normal, separable, non-metrizable Moore space.

Keywords

54D3554E3054E5254E9906B3506F99domain-representableScott-domain-representablemeasurementBurke's spacedevelopable spacesweakly developable spacesGδ-diagonalČech-complete spaceMoore spaceω1weakly developable spacesharp baseAF-complete
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 2 , 01 June 2011 , pp. 193 - 206
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Aarts, J. and Lutzer, D., Completeness properties designed for recognizing Baire spaces. Dissertationes Math. 116(1974).Google Scholar
[2] Alleche, B., Arhangelskii, A. V., and Calbrix, J., Weak developments and metrization. Topology Appl. 100(2000), no. 1, 23–38.Google Scholar
[3] Bennett, H. and Lutzer, D., Domain representable spaces. Fund. Math. 189(2006), no. 3, 255–268.Google Scholar
[4] Bennett, H. and Lutzer, D., Domain representable spaces and completeness. Topology Proc. 34(2009), 223–244.Google Scholar
[5] Bennett, H., Lutzer, D., and Reed, G. M., Domain representability and the Choquet game in Moore and BCO-spaces. Topology Appl. 155(2008), no. 5, 445–458.Google Scholar
[6] Burke, D. K., A nondevelopable locally compact Hausdorff space with a G δ -diagonal. General Topology and Appl. 2(1972), 287–291.Google Scholar
[7] Chaber, J., Conditions which imply compactness in countably compact spaces. Bull. Acad. Polon. Sci. Sér. Math. Astronom. Phys. 24(1976), no. 11, 993–998.Google Scholar
[8] Duke, K. and Lutzer, D., Scott domain representability of a class of generalized ordered spaces. Topology Proc. 32(2008), Spring, 1–14.Google Scholar
[9] Gierz, G., Hoffman, K. H., Keimal, K., Lawson, J. D., Mislove, M., and Scott, D., Continuous Lattices and Domains. Encyclopedia of Mathematics and its Applications, 93, Cambridge University Press, Cambridge, 2003.Google Scholar
[10] Gillman, L. and Jerrison, M., Rings of Continuous Functions. The University Series in Higher Mathematics, D. Van Nostrand, Princeton, NJ-Toronto-London-New York, 1960.Google Scholar
[11] Gruenhage, G., Generalized metric spaces. In: Handbook of Set-Theoretic Topology, North-Holland, Amsterdam, 1984, pp. 423–501.Google Scholar
[12] Kopperman, R., Künzi, H.-P., and Waszkiewicz, P., Bounded complete models of topological spaces. Topology Appl. 139(2004), no. 1–3, 285–297.Google Scholar
[13] Lutzer, D., On generalized ordered spaces. Dissertationes Math. Rozprawy Mat. 89(1971).Google Scholar
[14] Martin, K., Topological games in domain theory. Topology Appl. 129(2003), no. 2, 177–186.Google Scholar
[15] Martin, K., Ideal models of spaces. Topology in computer science. Theoret. Comput. Sci. 305(2003), no. 1–3, 277–297.Google Scholar
[16] Martin, K., A foundation for computation. Ph.D. Thesis, Tulane University, New Orleans, 2000.Google Scholar
[17] Martin, K., The measurement process in domain theory. In: Automata, languages and programming (Geneva, 2000), Lecture Notes in Comput. Sci., 1853, Springer, Berlin, 2000, pp. 116–126.Google Scholar
[18] Martin, K., Mislove, M., and Reed, G. M., Topology and domain theory. In: Recent progress in general topology, II, North-Holland, Amsterdam, 2002, pp. 371–394.Google Scholar
[19] Reed, G. M., Measurements on domains and topology. Electronic Notes in Theoretical Computer Science 40(2001), 303.Google Scholar
[20] Worrell, J. M., Jr. and Wicke, H. H., Characterizations of developable topological spaces. Canad. J. Math. 17(1965), 820–830.Google Scholar