Hostname: page-component-cd9895bd7-q99xh Total loading time: 0 Render date: 2024-12-26T20:16:08.440Z Has data issue: false hasContentIssue false
  • English
  • Français

The Mean Width of Circumscribed Random Polytopes

Published online by Cambridge University Press:  20 November 2018

Károly J. Böröczky  and
Rolf Schneider
Károly J. Böröczky
Affiliation:
Alfréd Rényi Institute of Mathematics, Hungarian Academy of Sciences, Budapest, Hungary, andDepartment of Geometry, Roland Eötvös University, Pázmány Péter sétány 1/C, Budapest, Hungary e-mail: [email protected]
Rolf Schneider
Affiliation:
Mathematisches Institut, Albert-Ludwigs-Universität, Freiburg i. Br., Germany e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

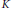For a given convex body $K$ in 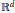${{\mathbb{R}}^{d}}$, a random polytope ${{K}^{(n)}}$ is defined (essentially) as the intersection of $n$ independent closed halfspaces containing 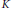$K$ and having an isotropic and (in a specified sense) uniform distribution. We prove upper and lower bounds of optimal orders for the difference of the mean widths of ${{K}^{(n)}}$ and 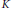$K$ as $n$ tends to infinity. For a simplicial polytope 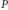$P$, a precise asymptotic formula for the difference of the mean widths of 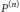${{P}^{(n)}}$ and 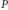$P$ is obtained.

Keywords

52A2260D0552A27random polytopemean widthapproximation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 4 , 01 December 2010 , pp. 614 - 628
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Affentranger, F., The convex hull of random points with spherically symmetric distributions. Rend. Sem. Mat. Univ. Politec. Torino 49(1991), no. 3, 359–383.Google Scholar
[2] Affentranger, F. and Wieacker, J. A., On the convex hull of uniform random points in a simple d-polytope. Discrete Comput. Geom. 6(1991), no. 4, 291–305. doi:10.1007/BF02574691Google Scholar
[3] Bárány, I., The technique of M-regions and cap-covering: a survey. Rend. Circ. Mat. Palermo (2) Suppl. 65(2000), part II, 21–38.Google Scholar
[4] Bárány, I., Random polytopes, convex bodies, and approximation. In: Stochastic geometry. Lecture Notes in Math, 1892, Springer, Berlin, 2007, pp. 77–118.Google Scholar
[5] Bárány, I. and Buchta, C., Random polytopes in a convex polytope, independence of shape, and concentration of vertices. Math. Ann. 297(1993), no. 3, 467–497. doi:10.1007/BF01459511Google Scholar
[6] Bárány, I. and Larman, D. G., Convex bodies, economic cap coverings, random polytopes. Mathematika 35(1988), no. 2, 274–291. doi:10.1112/S0025579300015266Google Scholar
[7] Böröczky, K. Jr. and Reitzner, M., Approximation of smooth convex bodies by random circumscribed polytopes. Ann. Appl. Probab. 14(2004), no. 1, 239–273. doi:10.1214/aoap/1075828053Google Scholar
[8] Buchta, C. and Reitzner, M., The convex hull of random points in a tetrahedron: solution of Blaschke's problem and more general results. J. Reine Angew. Math. 536(2001), 1–29.Google Scholar
[9] Efron, B., The convex hull of random set of points. Biometrika 52(1965), 331–343.Google Scholar
[10] Groemer, H., On the mean value of the volume of a random polytope in a convex set. Arch. Math. 25(1974), 86–90.Google Scholar
[11] Glasauer, S. and Gruber, P. M., Asymptotic estimates for best and stepwise approximation of convex bodies III. Forum Math. 9(1997), no. 4, 383–404. doi:10.1515/form.1997.9.383Google Scholar
[12] Gruber, P. M., Comparisons of best and random approximation of convex bodies by polytopes. II. Rend. Circ. Mat. Palermo (2) Suppl. 50(1997), 189–216.Google Scholar
[13] Gruber, P. M., Convex and discrete geometry. Fundamental Principles of Mathematical Sciences, 336, Springer, Berlin, 2007.Google Scholar
[14] Kaltenbach, F. J., Asymptotisches Verhalten zufälliger konvexer Polyeder. Doctoral Thesis, Freiburg 1990.Google Scholar
[15] Reed, W. J., Random points in a simplex. Pacific J. Math. 54(1974), no. 2, 183–198.Google Scholar
[16] Rényi, A. and Sulanke, R., Über die konvexe Hülle von n zufällig gewählten Punkten. Z. Wahrscheinlichkeitstheorie und Verw. Gebiete 2(1963), 75–84. doi:10.1007/BF00535300Google Scholar
[17] Rényi, A. and Sulanke, R., Über die konvexe Hülle von n zufällig gewählten Punkten, II. Z.Wahrscheinlichkeitstheorie und Verw. Gebiete 3(1964), 138–147. doi:10.1007/BF00535973Google Scholar
[18] Rényi, A. and Sulanke, R., Zufällige konvexe Polygone in einem Ringgebiet. Z.Wahrscheinlichkeitstheorie und Verw. Gebiete 9(1968), 146–157. doi:10.1007/BF01851005Google Scholar
[19] Schneider, R., Approximation of convex bodies by random polytopes. Aequationes Math. 32(1987), no. 2–3, 304–310. doi:10.1007/BF02311318Google Scholar
[20] Schneider, R., Convex bodies: the Brunn-Minkowski Theory. Encyclopedia of Mathematics and its Applications, 44, Cambridge University Press, Cambridge, 1993.Google Scholar
[21] Schneider, R., Discrete aspects of stochastic geometry. In: Handbook of discrete and computational geometry, second ed., CRC Press, Boca Raton, FL, 2004, pp. 255–278.Google Scholar
[22] Weil, W. and Wieacker, J. A., Stochastic geometry. In: Handbook of convex geometry, North-Holland, Amsterdam, 1993, pp. 1391–1438.Google Scholar
[23] Wieacker, J. A., Einige Probleme der polyedrischen Approximation. Diplomarbeit, University of Freiburg i. Br., 1978.Google Scholar
[24] Ziezold, H., Über die Eckenanzahl zufälliger konvexer Polygone. Izv. Akad. Nauk Armjan. SSR Ser. Mat. 5(1970), no. 3, 296–312.Google Scholar