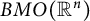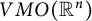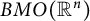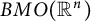1 Introduction
Let
![]() $A\subset \mathbb {R}^n$
be a measurable set with positive finite measure and
$A\subset \mathbb {R}^n$
be a measurable set with positive finite measure and
![]() $f\in {L}_{\mathrm{loc}}^1(\mathbb {R}^n)$
. By the mean oscillation of f on A, we mean the quantity
$f\in {L}_{\mathrm{loc}}^1(\mathbb {R}^n)$
. By the mean oscillation of f on A, we mean the quantity
where
and
![]() $f_A$
mean the average of f over A, i.e.,
$f_A$
mean the average of f over A, i.e.,
![]() $\frac {1}{|A|}\int _{A} f$
. Then it is said that f is of bounded mean oscillation if
$\frac {1}{|A|}\int _{A} f$
. Then it is said that f is of bounded mean oscillation if
![]() $O(f,Q)$
is uniformly bounded on all cubes Q (by a cube we mean a closed cube with sides parallel to the axes). The space of such functions is denoted by
$O(f,Q)$
is uniformly bounded on all cubes Q (by a cube we mean a closed cube with sides parallel to the axes). The space of such functions is denoted by
![]() ${BMO}(\mathbb {R}^n)$
, and modulo constants the following quantity defines a norm on this space:
${BMO}(\mathbb {R}^n)$
, and modulo constants the following quantity defines a norm on this space:
Sometimes we use
![]() $\|f\|_{BMO(Q_0)}$
, which means that we take the above supremum over all cubes contained in
$\|f\|_{BMO(Q_0)}$
, which means that we take the above supremum over all cubes contained in
![]() $Q_0$
.
$Q_0$
.
![]() ${BMO}(\mathbb {R}^n)$
is a Banach space and since its introduction has played an important role in harmonic analysis. It is the dual of the Hardy space
${BMO}(\mathbb {R}^n)$
is a Banach space and since its introduction has played an important role in harmonic analysis. It is the dual of the Hardy space
![]() ${H}^1(\mathbb {R}^n)$
, and it contains
${H}^1(\mathbb {R}^n)$
, and it contains
![]() ${L}^{\infty }(\mathbb {R}^n)$
and somehow serves as a substitute for it. For instance, Calderón–Zygmund singular integral operators map
${L}^{\infty }(\mathbb {R}^n)$
and somehow serves as a substitute for it. For instance, Calderón–Zygmund singular integral operators map
![]() ${BMO}(\mathbb {R}^n)$
to itself, and consequently these operators map
${BMO}(\mathbb {R}^n)$
to itself, and consequently these operators map
![]() ${L}^{\infty }(\mathbb {R}^n)$
to
${L}^{\infty }(\mathbb {R}^n)$
to
![]() ${BMO}(\mathbb {R}^n)$
but not to itself [Reference García-Cuerva and Francia5].
${BMO}(\mathbb {R}^n)$
but not to itself [Reference García-Cuerva and Francia5].
Another important class of operators is the class of maximal operators, and the first objective of the present paper is to investigate the action of some of these operators on
![]() ${BMO}(\mathbb {R}^n)$
. Let us recall that the uncentered Hardy–Littlewood maximal operator is defined by
${BMO}(\mathbb {R}^n)$
. Let us recall that the uncentered Hardy–Littlewood maximal operator is defined by
where the above supremum is taken over all cubes containing x. As it is well known, M is of weak-type
![]() $(1,1)$
and bounded on
$(1,1)$
and bounded on
![]() ${L}^p(\mathbb {R}^n)$
for
${L}^p(\mathbb {R}^n)$
for
![]() $1<p\le \infty $
[Reference García-Cuerva and Francia5]. For a function
$1<p\le \infty $
[Reference García-Cuerva and Francia5]. For a function
![]() $f \in {BMO}(\mathbb {R}^n)$
, it might be the case that
$f \in {BMO}(\mathbb {R}^n)$
, it might be the case that
![]() $Mf$
is identically equal to infinity. For instance, this is the case when
$Mf$
is identically equal to infinity. For instance, this is the case when
![]() $f(x)=\log |x|$
. However, in [Reference Bennett, DeVore and Sharpley2], the authors proved that if this is not the case, then
$f(x)=\log |x|$
. However, in [Reference Bennett, DeVore and Sharpley2], the authors proved that if this is not the case, then
![]() $Mf$
belongs to
$Mf$
belongs to
![]() ${BMO}(\mathbb {R}^n)$
, and for a dimensional constant
${BMO}(\mathbb {R}^n)$
, and for a dimensional constant
![]() $c(n)$
, we have
$c(n)$
, we have
Another proof of this was given in [Reference Bennett1], and a third one in [Reference Saari12], where the author proved that M preserves Poincaré inequalities. Regarding this, we ask the following question about the continuity of the uncentered Hardy–Littlewood maximal operator on
![]() ${BMO}(\mathbb {R}^n)$
.
${BMO}(\mathbb {R}^n)$
.
Question 1.1 Let
![]() $f\in {L}^{\infty }(\mathbb {R}^n)$
, and let
$f\in {L}^{\infty }(\mathbb {R}^n)$
, and let
![]() $\{f_k\}$
be a sequence of bounded functions converging to f in
$\{f_k\}$
be a sequence of bounded functions converging to f in
![]() ${BMO}(\mathbb {R}^n)$
. Is it true that
${BMO}(\mathbb {R}^n)$
. Is it true that
![]() $\{Mf_k\}$
converges to
$\{Mf_k\}$
converges to
![]() $Mf$
in
$Mf$
in
![]() ${BMO}(\mathbb {R}^n)$
?
${BMO}(\mathbb {R}^n)$
?
The operator M is nonlinear, and for such operators, continuity does not follow from boundedness. However, it is pointwise sublinear and this makes it continuous on
![]() ${L}^p(\mathbb {R}^n)$
for
${L}^p(\mathbb {R}^n)$
for
![]() $1<p\le \infty $
. In [Reference Luiro11], a similar question has been studied for Sobolev spaces, where the author proved that M is continuous on
$1<p\le \infty $
. In [Reference Luiro11], a similar question has been studied for Sobolev spaces, where the author proved that M is continuous on
![]() $W^{1,p}(\mathbb {R}^n)$
for
$W^{1,p}(\mathbb {R}^n)$
for
![]() $1<p<\infty $
. However, in Section 2, we give a negative answer to the above question.
$1<p<\infty $
. However, in Section 2, we give a negative answer to the above question.
![]() ${BMO}(\mathbb {R}^n)$
has an important subspace, namely
${BMO}(\mathbb {R}^n)$
has an important subspace, namely
![]() ${VMO}(\mathbb {R}^n)$
or functions of vanishing mean oscillation.
${VMO}(\mathbb {R}^n)$
or functions of vanishing mean oscillation.
![]() ${VMO}(\mathbb {R}^n)$
is the closure of the uniformly continuous functions in
${VMO}(\mathbb {R}^n)$
is the closure of the uniformly continuous functions in
![]() ${BMO}(\mathbb {R}^n)$
. Another characterization of
${BMO}(\mathbb {R}^n)$
. Another characterization of
![]() ${VMO}(\mathbb {R}^n)$
is given in terms of the modulus of mean oscillation which is defined by
${VMO}(\mathbb {R}^n)$
is given in terms of the modulus of mean oscillation which is defined by
and
![]() $f\in {VMO}(\mathbb {R}^n)$
exactly when
$f\in {VMO}(\mathbb {R}^n)$
exactly when
![]() $\lim \limits _{\delta \to 0}\omega (f, \delta )=0$
(in the above by
$\lim \limits _{\delta \to 0}\omega (f, \delta )=0$
(in the above by
![]() $l(Q)$
we mean the side length of Q)[Reference Sarason13]. Regarding this subspace, we ask the following question.
$l(Q)$
we mean the side length of Q)[Reference Sarason13]. Regarding this subspace, we ask the following question.
Question 1.2 Let
![]() $f\in {VMO}(\mathbb {R}^n)$
such that
$f\in {VMO}(\mathbb {R}^n)$
such that
![]() $Mf$
is not identically equal to infinity. Is it true that
$Mf$
is not identically equal to infinity. Is it true that
![]() $Mf \in {VMO}(\mathbb {R}^n)$
?
$Mf \in {VMO}(\mathbb {R}^n)$
?
In Section 3, we provide a positive answer to this question.
In Section 4, we consider the action of some other maximal operators on
![]() ${BMO}(\mathbb {R}^n)$
. More specifically, the directional maximal operator in the direction
${BMO}(\mathbb {R}^n)$
. More specifically, the directional maximal operator in the direction
![]() $e_1=(1,0,\ldots ,0)$
,
$e_1=(1,0,\ldots ,0)$
,
![]() $M_{e_1}$
, and the strong maximal operator,
$M_{e_1}$
, and the strong maximal operator,
![]() $M_s$
, which are defined as the following:
$M_s$
, which are defined as the following:
In the above,
![]() $f_{x'}(t):=f(t,x')$
, where
$f_{x'}(t):=f(t,x')$
, where
![]() $(t,x')\in \mathbb {R}\times \mathbb {R}^{n-1}$
, and the left supremum is taken over all closed intervals containing
$(t,x')\in \mathbb {R}\times \mathbb {R}^{n-1}$
, and the left supremum is taken over all closed intervals containing
![]() $x_1$
. In a similar way, one can define the directional maximal operator
$x_1$
. In a similar way, one can define the directional maximal operator
![]() $M_e$
, which is taken in the direction
$M_e$
, which is taken in the direction
![]() $e\in \mathbb {S}^{n-1}$
, simply by taking the one-dimensional uncentered Hardy–Littlewood maximal operator on every line in direction e. However, since
$e\in \mathbb {S}^{n-1}$
, simply by taking the one-dimensional uncentered Hardy–Littlewood maximal operator on every line in direction e. However, since
![]() ${BMO}(\mathbb {R}^n)$
is invariant under rotations, it is enough to study
${BMO}(\mathbb {R}^n)$
is invariant under rotations, it is enough to study
![]() $M_{e_1}$
. In the above, the right supremum is taken over all rectangles containing x, and by a rectangle, we mean a closed rectangle with sides parallel to the axes. These are the most important maximal operators in multiparameter harmonic analysis and are bounded and continuous on
$M_{e_1}$
. In the above, the right supremum is taken over all rectangles containing x, and by a rectangle, we mean a closed rectangle with sides parallel to the axes. These are the most important maximal operators in multiparameter harmonic analysis and are bounded and continuous on
![]() ${L}^p(\mathbb {R}^n)$
for
${L}^p(\mathbb {R}^n)$
for
![]() $1<p\le \infty $
[Reference Chang and Fefferman3]. Regarding these operators, we ask the following question.
$1<p\le \infty $
[Reference Chang and Fefferman3]. Regarding these operators, we ask the following question.
Question 1.3 Are there constants
![]() $C, C'\ge 1$
such that at least for every bounded function f the following inequalities hold?
$C, C'\ge 1$
such that at least for every bounded function f the following inequalities hold?
To answer this question, we have to study the properties of slices of functions in
![]() ${BMO}(\mathbb {R}^n)$
, which is the second objective of this paper. Many function spaces have the property that their slices lie in the same scale of spaces. For example, almost every slice of a function in
${BMO}(\mathbb {R}^n)$
, which is the second objective of this paper. Many function spaces have the property that their slices lie in the same scale of spaces. For example, almost every slice of a function in
![]() ${L}^p(\mathbb {R}^n)$
or
${L}^p(\mathbb {R}^n)$
or
![]() $W^{1,p}(\mathbb {R}^n)$
lies in
$W^{1,p}(\mathbb {R}^n)$
lies in
![]() $L^p(\mathbb {R}^{n-1})$
or
$L^p(\mathbb {R}^{n-1})$
or
![]() $W^{1,p}(\mathbb {R}^{n-1})$
, respectively [Reference Leoni10]. The same is true for
$W^{1,p}(\mathbb {R}^{n-1})$
, respectively [Reference Leoni10]. The same is true for
![]() $BMO_s(\mathbb {R}^n)$
, strong
$BMO_s(\mathbb {R}^n)$
, strong
![]() $BMO$
, which is the subspace of
$BMO$
, which is the subspace of
![]() ${BMO}(\mathbb {R}^n)$
consisting of all functions with bounded mean oscillation on rectangles[Reference Dafni and Gibara4]. This property is also satisfied by the scale of homogeneous Lipschitz spaces
${BMO}(\mathbb {R}^n)$
consisting of all functions with bounded mean oscillation on rectangles[Reference Dafni and Gibara4]. This property is also satisfied by the scale of homogeneous Lipschitz spaces
![]() $\dot {\Lambda }^{n(\frac {1}{p}-1)}(\mathbb {R}^{n})$
, the duals of
$\dot {\Lambda }^{n(\frac {1}{p}-1)}(\mathbb {R}^{n})$
, the duals of
![]() ${H}^p(\mathbb {R}^n)$
for
${H}^p(\mathbb {R}^n)$
for
![]() $0<p<1$
[Reference García-Cuerva and Francia5]. Regarding this, we ask our last question.
$0<p<1$
[Reference García-Cuerva and Francia5]. Regarding this, we ask our last question.
Question 1.4 Is it true that almost every horizontal or vertical slice of a function in
![]() ${BMO}(\mathbb {R}^2)$
belongs to
${BMO}(\mathbb {R}^2)$
belongs to
![]() ${BMO}(\mathbb {R})$
?
${BMO}(\mathbb {R})$
?
In Section 4, we answer both questions negatively, and in the last theorem of this paper, we prove a property of the slices of functions in
![]() ${BMO}(\mathbb {R}^2)$
.
${BMO}(\mathbb {R}^2)$
.
Before we proceed further, let us fix some notation. By
![]() $A\lesssim B$
,
$A\lesssim B$
,
![]() $A\gtrsim B$
, and
$A\gtrsim B$
, and
![]() $A\approx B$
, we mean
$A\approx B$
, we mean
![]() $A\le CB$
,
$A\le CB$
,
![]() $A\ge CB$
, and
$A\ge CB$
, and
![]() $C^{-1}B\le A \le CB$
, respectively, where C is a constant independent of the important parameters.
$C^{-1}B\le A \le CB$
, respectively, where C is a constant independent of the important parameters.
2 Discontinuity of M on
 ${BMO}(\mathbb {R}^n)$
${BMO}(\mathbb {R}^n)$
Our theorem in this section is the following.
Theorem 2.1 Let f be a nonnegative function supported in
![]() $[0,1]$
,
$[0,1]$
,
![]() $\|f\|_{{L}^{\infty }}\le 1$
, and
$\|f\|_{{L}^{\infty }}\le 1$
, and
![]() $\|f\|_{{L}^1}>\log 2$
. Then, there exists a sequence of bounded functions
$\|f\|_{{L}^1}>\log 2$
. Then, there exists a sequence of bounded functions
![]() $\{f_n\}$
converging to f in
$\{f_n\}$
converging to f in
![]() ${BMO}(\mathbb {R})$
such that
${BMO}(\mathbb {R})$
such that
![]() $\{Mf_n\}$
does not converge to
$\{Mf_n\}$
does not converge to
![]() $Mf$
in
$Mf$
in
![]() ${BMO}(\mathbb {R})$
.
${BMO}(\mathbb {R})$
.
To prove this, we need a couple of simple lemmas which we give below.
Lemma 2.2 Let
![]() $T>0$
and
$T>0$
and
![]() $h \in BMO[0,\frac {T}{2}]$
. Then the even periodic extension of h, which is defined by
$h \in BMO[0,\frac {T}{2}]$
. Then the even periodic extension of h, which is defined by
is in
![]() ${BMO}(\mathbb {R})$
and
${BMO}(\mathbb {R})$
and
![]() $\|H\|_{{{BMO}(\mathbb {R})}}\le 10\|h\|_{BMO[0,\frac {T}{2}]}$
.
$\|H\|_{{{BMO}(\mathbb {R})}}\le 10\|h\|_{BMO[0,\frac {T}{2}]}$
.
Proof For an arbitrary interval I, there are two possibilities:
-
(i)
 $|I|\le \frac {T}{2}$
.
$|I|\le \frac {T}{2}$
.
In this case by a translation by an integer multiple of T and using periodicity of H, we may assume either
![]() $I\subset [-\frac {T}{2},\frac {T}{2}]$
or
$I\subset [-\frac {T}{2},\frac {T}{2}]$
or
![]() $I\subset [0,T]$
. Suppose
$I\subset [0,T]$
. Suppose
![]() $I\subset [-\frac {T}{2},\frac {T}{2}]$
and note that if
$I\subset [-\frac {T}{2},\frac {T}{2}]$
and note that if
![]() $0\notin I$
, we have either
$0\notin I$
, we have either
![]() $I\subset [0,\frac {T}{2}]$
or
$I\subset [0,\frac {T}{2}]$
or
![]() $I\subset [-\frac {T}{2},0]$
and from the symmetry
$I\subset [-\frac {T}{2},0]$
and from the symmetry
![]() $O(H,I)\le \|h\|_{BMO[0,\frac {T}{2}]}$
. If
$O(H,I)\le \|h\|_{BMO[0,\frac {T}{2}]}$
. If
![]() $0\in I$
, then take the interval J centered at zero with the right half
$0\in I$
, then take the interval J centered at zero with the right half
![]() $J^+$
, which contains I and
$J^+$
, which contains I and
![]() $|J|\le 2 |I|.$
Again from symmetry, we get
$|J|\le 2 |I|.$
Again from symmetry, we get
The same argument works for
![]() $I\subset [0,T]$
. This time we use the symmetry of H around
$I\subset [0,T]$
. This time we use the symmetry of H around
![]() $\frac {T}{2}$
.
$\frac {T}{2}$
.
-
(ii)
 $|I|\ge \frac {T}{2}$
.
$|I|\ge \frac {T}{2}$
.
This time take
![]() $J=[nT,mT]$
with
$J=[nT,mT]$
with
![]() $n,m \in \mathbb {Z}$
which contains I and
$n,m \in \mathbb {Z}$
which contains I and
![]() $|J|\le |I|+2T\le 5|I|$
. And again like the previous cases, from the symmetry and periodicity of H, we get
$|J|\le |I|+2T\le 5|I|$
. And again like the previous cases, from the symmetry and periodicity of H, we get
The proof is now complete.
In the above, the norm of the extension operator is independent of T, and we will use this in the proof of the next lemma.
Remark 2.3 There are much more general ways to extend
![]() $BMO$
functions to the outside of domains, but for the purpose of our paper, the above simple lemma is enough. See [Reference Jones8] for more on extensions.
$BMO$
functions to the outside of domains, but for the purpose of our paper, the above simple lemma is enough. See [Reference Jones8] for more on extensions.
Lemma 2.4 For
![]() $c<-1$
, there exists a sequence of functions
$c<-1$
, there exists a sequence of functions
![]() $\{g_n\}$
,
$\{g_n\}$
,
![]() $n\ge 1$
with the following properties:
$n\ge 1$
with the following properties:
-
(1)
 $g_n\ge 0$
,
$g_n\ge 0$
, -
(2)
 $g_n=0$
on
$g_n=0$
on
 $[c,1]$
,
$[c,1]$
, -
(3)
 $\|g_n\|_{{L}^{\infty }}\le 1$
,
$\|g_n\|_{{L}^{\infty }}\le 1$
, -
(4)
 ,
, -
(5)
 $\lim \limits _{n\to \infty }\|g_n\|_{{{BMO}(\mathbb {R})}}=0$
.
$\lim \limits _{n\to \infty }\|g_n\|_{{{BMO}(\mathbb {R})}}=0$
.
Proof Let
![]() $\log ^+|x|=\max \{0, \log |x|\}$
be the positive part of the logarithm, and consider the function
$\log ^+|x|=\max \{0, \log |x|\}$
be the positive part of the logarithm, and consider the function
![]() $h_n(x)=\log ^+x$
on the interval
$h_n(x)=\log ^+x$
on the interval
![]() $[0,n]$
, which belongs to
$[0,n]$
, which belongs to
![]() $BMO[0,n]$
with
$BMO[0,n]$
with
![]() $\|h_n\|_{BMO[0,n]}\le \|\log ^+|\cdot |\|_{{{BMO}(\mathbb {R})}}$
. Then an application of Lemma 2.2 with
$\|h_n\|_{BMO[0,n]}\le \|\log ^+|\cdot |\|_{{{BMO}(\mathbb {R})}}$
. Then an application of Lemma 2.2 with
![]() $T=2n$
gives us a sequence of nonnegative functions
$T=2n$
gives us a sequence of nonnegative functions
![]() $H_n$
with
$H_n$
with
![]() $\|H_n\|_{{{BMO}(\mathbb {R})}}\lesssim 1$
(here our bounds are independent of n). Now, let
$\|H_n\|_{{{BMO}(\mathbb {R})}}\lesssim 1$
(here our bounds are independent of n). Now, let
![]() $g_n=\frac {1}{1+\log n}H_n(x)\left (1-\chi _{[c,0]}(x)\right )$
. Then, the first three properties are immediate from the definition, the forth one follows from integration, and the last one from
$g_n=\frac {1}{1+\log n}H_n(x)\left (1-\chi _{[c,0]}(x)\right )$
. Then, the first three properties are immediate from the definition, the forth one follows from integration, and the last one from
 $$\begin{align*}\|g_n\|_{{{BMO}(\mathbb{R})}}\le \frac{1}{1+\log n}\left(\|H_n\|_{{{BMO}(\mathbb{R})}}+\|H_n\chi_{[c,0]}\|_{{L}^{\infty}}\right)\lesssim\frac{\log|c|}{1+\log n} \quad n\ge1. \end{align*}$$
$$\begin{align*}\|g_n\|_{{{BMO}(\mathbb{R})}}\le \frac{1}{1+\log n}\left(\|H_n\|_{{{BMO}(\mathbb{R})}}+\|H_n\chi_{[c,0]}\|_{{L}^{\infty}}\right)\lesssim\frac{\log|c|}{1+\log n} \quad n\ge1. \end{align*}$$
This finishes the proof.
Now, we turn to the proof of the above theorem.
Proof of Theorem 2.1
Let f be as in the theorem,
![]() $a=\int _{0}^{1}f$
,
$a=\int _{0}^{1}f$
,
![]() $c<0$
a constant with large magnitude to be determined later, and let
$c<0$
a constant with large magnitude to be determined later, and let
![]() $g_n$
be the sequence constructed in Lemma 2.4.
$g_n$
be the sequence constructed in Lemma 2.4.
We will show that
This proves the theorem once we note that since f and
![]() $g_n$
are bounded functions,
$g_n$
are bounded functions,
![]() $f_n$
is bounded too. Also, from the fifth property of
$f_n$
is bounded too. Also, from the fifth property of
![]() $\{g_n\}$
in the above lemma,
$\{g_n\}$
in the above lemma,
![]() $\{f_n\}$
converges to f in
$\{f_n\}$
converges to f in
![]() ${BMO}(\mathbb {R})$
.
${BMO}(\mathbb {R})$
.
To begin with, we claim that
![]() $Mf_n=Mf$
on
$Mf_n=Mf$
on
![]() $[c,0]$
. To see this, note that from the positivity of f and
$[c,0]$
. To see this, note that from the positivity of f and
![]() $g_n$
,
$g_n$
,
![]() $Mf_n(x)\ge Mf(x)$
for all values of x, and it remains to show that the reverse inequality holds also. For
$Mf_n(x)\ge Mf(x)$
for all values of x, and it remains to show that the reverse inequality holds also. For
![]() $x \in [c,0]$
,
$x \in [c,0]$
,
![]() $Mf(x)\ge \frac {\int _{c}^{1}f}{1-c}=\frac {a}{1-c}$
, and for any interval I which contains x, we have two possibilities:
$Mf(x)\ge \frac {\int _{c}^{1}f}{1-c}=\frac {a}{1-c}$
, and for any interval I which contains x, we have two possibilities:
-
(i) either
 $I\subset (-\infty ,0)$
, in which case from the third property of
$I\subset (-\infty ,0)$
, in which case from the third property of
 $g_n$
we have
$g_n$
we have 
-
(ii) or
 $I\cap [0,1]\ne \emptyset $
, in which case the second and third properties of
$I\cap [0,1]\ne \emptyset $
, in which case the second and third properties of
 $g_n$
give us
$g_n$
give us 
This proves our claim.
Next, we look at the mean oscillation of
![]() $Mf_n-Mf$
on
$Mf_n-Mf$
on
![]() $[2c,0]$
. Because this function vanishes on
$[2c,0]$
. Because this function vanishes on
![]() $[c,0]$
, we have
$[c,0]$
, we have
To bound the right-hand side of the above inequality from below, we note that
![]() $0\le f\le \chi _{[0,1]}$
, so
$0\le f\le \chi _{[0,1]}$
, so
![]() $Mf(x)\le M(\chi _{[0,1]})(x)=\frac {1}{1-x}$
for
$Mf(x)\le M(\chi _{[0,1]})(x)=\frac {1}{1-x}$
for
![]() $x\le 0$
. Also, for
$x\le 0$
. Also, for
![]() $x\le 0$
, we have
$x\le 0$
, we have
So, we get the following estimate for the right-hand side in (3):
Combining (3) and (4) gives us
Now, taking the limit inferior as
![]() $n\to \infty $
and using the forth property of
$n\to \infty $
and using the forth property of
![]() $g_n$
give us
$g_n$
give us
This shows that if we have
then (2) holds. Here, we note that the function on the right-hand side of (5) attains its minimum, which is
![]() $\log 2$
, at infinity. Also, from the assumption,
$\log 2$
, at infinity. Also, from the assumption,
![]() $a>\log 2$
, so if we choose
$a>\log 2$
, so if we choose
![]() $|c|$
sufficiently large, (5) holds, and this completes the proof.
$|c|$
sufficiently large, (5) holds, and this completes the proof.
By lifting the above functions to higher dimensions with
we obtain a counterexample for continuity of the n-dimensional uncentered Hardy–Littlewood maximal operator on
![]() ${BMO}(\mathbb {R}^n)$
, simply because the
${BMO}(\mathbb {R}^n)$
, simply because the
![]() ${BMO}(\mathbb {R}^n)$
norms and the maximal operator become one-dimensional.
${BMO}(\mathbb {R}^n)$
norms and the maximal operator become one-dimensional.
Corollary 2.5 The uncentered Hardy–Littlewood maximal operator is bounded on
![]() ${L}^{\infty }(\mathbb {R}^n)$
equipped with the
${L}^{\infty }(\mathbb {R}^n)$
equipped with the
![]() $BMO$
norm, but it is not continuous.
$BMO$
norm, but it is not continuous.
3 The uncentered Hardy–Littlewood maximal operator on
 ${VMO}(\mathbb {R}^n)$
${VMO}(\mathbb {R}^n)$
As it was mentioned before,
![]() ${VMO}(\mathbb {R}^n)$
is the
${VMO}(\mathbb {R}^n)$
is the
![]() ${BMO}(\mathbb {R}^n)$
-closure of the uniformly continuous functions which belong to
${BMO}(\mathbb {R}^n)$
-closure of the uniformly continuous functions which belong to
![]() ${BMO}(\mathbb {R}^n)$
. The operator M reduces modulus of continuity, because it is pointwise sublinear, so it preserves uniformly continuous functions. But from our previous result, one cannot deduce boundedness of M on
${BMO}(\mathbb {R}^n)$
. The operator M reduces modulus of continuity, because it is pointwise sublinear, so it preserves uniformly continuous functions. But from our previous result, one cannot deduce boundedness of M on
![]() ${VMO}(\mathbb {R}^n)$
by a limiting argument. Nevertheless, we have the following theorem.
${VMO}(\mathbb {R}^n)$
by a limiting argument. Nevertheless, we have the following theorem.
Theorem 3.1 Let
![]() $f \in {VMO}(\mathbb {R}^n)$
and suppose
$f \in {VMO}(\mathbb {R}^n)$
and suppose
![]() $Mf$
is not identically equal to infinity. Then
$Mf$
is not identically equal to infinity. Then
![]() $Mf$
belongs to
$Mf$
belongs to
![]() ${VMO}(\mathbb {R}^n)$
.
${VMO}(\mathbb {R}^n)$
.
Before we prove this, we bring the following lemma, which is needed later.
Lemma 3.2 Let A be a measurable subset of a cube Q of positive measure and
![]() $f\in {BMO}(\mathbb {R}^n)$
with
$f\in {BMO}(\mathbb {R}^n)$
with
![]() $\|f\|_{{BMO}(\mathbb {R}^n)}=1$
; then we have
$\|f\|_{{BMO}(\mathbb {R}^n)}=1$
; then we have
Proof From the John–Nirenberg inequality [Reference John and Nirenberg7], there is a dimensional constant
![]() $c>0$
such that
$c>0$
such that
Now, Jensen’s inequality gives us (7), as follows:
Remark 3.3 In the above lemma, let A be a rectangle and take Q to be the smallest cube which contains it. Then
where
![]() $e(A)$
is the eccentricity of A, or the ratio of the largest side to the smallest one.
$e(A)$
is the eccentricity of A, or the ratio of the largest side to the smallest one.
We now turn to the proof of Theorem 3.1.
Proof of Theorem 3.1
Let f be as in the theorem, then we have to show that
![]() $ \varlimsup\limits_{\delta \to 0}\omega (Mf,\delta )=0$
. Now, for every cube Q, we have
$ \varlimsup\limits_{\delta \to 0}\omega (Mf,\delta )=0$
. Now, for every cube Q, we have
![]() $O(|f|,Q)\le 2O(f,Q)$
, which means that
$O(|f|,Q)\le 2O(f,Q)$
, which means that
![]() $|f|\in {VMO}(\mathbb {R}^n)$
too. From this together with
$|f|\in {VMO}(\mathbb {R}^n)$
too. From this together with
![]() $M(|f|)=Mf$
, it is enough to prove the theorem for nonnegative functions. Also, from the homogeneity of M, we may assume
$M(|f|)=Mf$
, it is enough to prove the theorem for nonnegative functions. Also, from the homogeneity of M, we may assume
![]() $\|f\|_{{BMO}(\mathbb {R}^n)}=1$
.
$\|f\|_{{BMO}(\mathbb {R}^n)}=1$
.
Let
![]() $Q_0$
be a cube and c a constant with
$Q_0$
be a cube and c a constant with
![]() $c>e$
. We decompose M into the local part,
$c>e$
. We decompose M into the local part,
![]() $M_1$
, and the nonlocal part,
$M_1$
, and the nonlocal part,
![]() $M_2$
, as follows:
$M_2$
, as follows:
 $$ \begin{align*} M_1f(x):=\underset{l(Q)\le cl(Q_0)}{\underset{x\in Q}\sup f_Q}, \quad \quad M_2f(x):=\underset{l(Q)\ge cl(Q_0)}{\underset{x\in Q}\sup f_Q}. \end{align*} $$
$$ \begin{align*} M_1f(x):=\underset{l(Q)\le cl(Q_0)}{\underset{x\in Q}\sup f_Q}, \quad \quad M_2f(x):=\underset{l(Q)\ge cl(Q_0)}{\underset{x\in Q}\sup f_Q}. \end{align*} $$
We have
![]() $Mf(x)=\max \{M_1f(x),M_2f(x)\}$
and so
$Mf(x)=\max \{M_1f(x),M_2f(x)\}$
and so
To estimate the first term in the right-hand side of (8), let
![]() $Q_0^*$
be the concentric dilation of
$Q_0^*$
be the concentric dilation of
![]() $Q_0$
with
$Q_0$
with
![]() $l(Q_0^*)=2cl(Q_0)$
. Then, for the local part, we have
$l(Q_0^*)=2cl(Q_0)$
. Then, for the local part, we have

By using the boundedness of M on
![]() $L^2(\mathbb {R}^n)$
, we get
$L^2(\mathbb {R}^n)$
, we get

and an application of the John–Nirenberg inequality gives us
To estimate the mean oscillation of the nonlocal part, suppose
![]() $x,y\in Q_0$
,
$x,y\in Q_0$
,
![]() $M_2f(x)>M_2f(y)$
and let Q be a cube with
$M_2f(x)>M_2f(y)$
and let Q be a cube with
![]() $l(Q)\ge cl(Q_0)$
, which contains x and such that
$l(Q)\ge cl(Q_0)$
, which contains x and such that
![]() $M_2f(y)<f_Q$
. Now, let
$M_2f(y)<f_Q$
. Now, let
![]() $Q'$
be a cube such that
$Q'$
be a cube such that
![]() $Q_0\cup Q\subset Q'$
,
$Q_0\cup Q\subset Q'$
,
![]() $l(Q')=l(Q)+l(Q_0)$
, and let
$l(Q')=l(Q)+l(Q_0)$
, and let
![]() $A=Q'\backslash Q$
. Then
$A=Q'\backslash Q$
. Then
![]() $M_2f(y)\ge f_{Q'}$
and we have
$M_2f(y)\ge f_{Q'}$
and we have

Here, we note that
![]() $|A|=|Q'|-|Q|\approx l(Q_0)l(Q)^{n-1}$
, and
$|A|=|Q'|-|Q|\approx l(Q_0)l(Q)^{n-1}$
, and
![]() $l(Q')\approx l(Q)$
. So, from the above inequality and Lemma 3.2, we get
$l(Q')\approx l(Q)$
. So, from the above inequality and Lemma 3.2, we get
 $$ \begin{align*} f_Q-M_2f(y)\lesssim \frac{l(Q_0)}{l(Q)}\left(1+\log\frac{l(Q)}{l(Q_0)}\right)\lesssim c^{-1}\log c. \end{align*} $$
$$ \begin{align*} f_Q-M_2f(y)\lesssim \frac{l(Q_0)}{l(Q)}\left(1+\log\frac{l(Q)}{l(Q_0)}\right)\lesssim c^{-1}\log c. \end{align*} $$
The reason for the last inequality is that
![]() $\frac {l(Q_0)}{l(Q)}\le c^{-1}$
and the function
$\frac {l(Q_0)}{l(Q)}\le c^{-1}$
and the function
![]() $-t\log t$
is increasing when
$-t\log t$
is increasing when
![]() $t<e^{-1}$
. Finally, by taking the supremum over all such cubes Q, we obtain
$t<e^{-1}$
. Finally, by taking the supremum over all such cubes Q, we obtain
So, for the nonlocal part, we have

By putting (8)–(10) together, we get
and taking the supremum over all cubes
![]() $Q_0$
with
$Q_0$
with
![]() $l(Q_0)\le \delta $
gives us
$l(Q_0)\le \delta $
gives us
To finish the proof, it is enough to take the limit superior as
![]() $\delta \to 0$
first, and then let
$\delta \to 0$
first, and then let
![]() $c\to \infty $
.
$c\to \infty $
.
Remark 3.4 The above argument shows that for all functions in
![]() ${BMO}(\mathbb {R}^n)$
, if one chooses a sufficiently large localization of M, (10) holds, meaning that the mean oscillation of the nonlocal part is small. This also shows itself in the dyadic setting: if one considers the dyadic maximal operator
${BMO}(\mathbb {R}^n)$
, if one chooses a sufficiently large localization of M, (10) holds, meaning that the mean oscillation of the nonlocal part is small. This also shows itself in the dyadic setting: if one considers the dyadic maximal operator
![]() $M^d$
and dyadic
$M^d$
and dyadic
![]() $BMO$
, denoted by
$BMO$
, denoted by
![]() ${BMO_d}(\mathbb {R}^n)$
, then for a dyadic cube
${BMO_d}(\mathbb {R}^n)$
, then for a dyadic cube
![]() $Q_0$
,
$Q_0$
,
 $$\begin{align*}M^{d}_2f(x)=\underset{l(Q)\ge l(Q_0)}{\underset{x\in Q}\sup f_Q}=\sup_{Q_0\subset Q}f_Q, \quad x\in Q_0. \end{align*}$$
$$\begin{align*}M^{d}_2f(x)=\underset{l(Q)\ge l(Q_0)}{\underset{x\in Q}\sup f_Q}=\sup_{Q_0\subset Q}f_Q, \quad x\in Q_0. \end{align*}$$
Hence,
![]() $O(M^{d}_2f,Q_0)=0$
, and therefore no dilation is needed
$O(M^{d}_2f,Q_0)=0$
, and therefore no dilation is needed
![]() $(c=1)$
.
$(c=1)$
.
4 Slices of BMO functions and unboundedness of directional and strong maximal operators
In this final section, we discuss properties of slices of functions in
![]() ${BMO}(\mathbb {R}^n)$
, and for simplicity, we restrict ourselves to
${BMO}(\mathbb {R}^n)$
, and for simplicity, we restrict ourselves to
![]() ${BMO}(\mathbb {R}^2)$
. We begin by asking the following question.
${BMO}(\mathbb {R}^2)$
. We begin by asking the following question.
Question Suppose
![]() $\varphi , \psi $
are two functions of one variable, when does
$\varphi , \psi $
are two functions of one variable, when does
![]() $f(x,y)=\varphi (x)\psi (y)$
belong to
$f(x,y)=\varphi (x)\psi (y)$
belong to
![]() ${BMO}(\mathbb {R}^2)$
?
${BMO}(\mathbb {R}^2)$
?
To answer this, we need the following lemma, which is an application of Fubini’s theorem and its proof is found in [Reference Dafni and Gibara4].
Lemma 4.1 Let
![]() $A, B \subset \mathbb {R}$
be two measurable sets with finite positive measure, and let f be a measurable function on
$A, B \subset \mathbb {R}$
be two measurable sets with finite positive measure, and let f be a measurable function on
![]() $\mathbb {R}^2$
. Then
$\mathbb {R}^2$
. Then
Now, take two intervals
![]() $I, J$
with
$I, J$
with
![]() $l(I)=l(J)$
. Then, an application of the above lemma to
$l(I)=l(J)$
. Then, an application of the above lemma to
![]() $f(x,y)=\varphi (x)\psi (y)$
gives us
$f(x,y)=\varphi (x)\psi (y)$
gives us
Taking the supremum over all such
![]() $I,J$
, we obtain
$I,J$
, we obtain

When
![]() $f\in {BMO}(\mathbb {R}^2)$
is nonzero on a set of positive measure, the above condition implies that
$f\in {BMO}(\mathbb {R}^2)$
is nonzero on a set of positive measure, the above condition implies that
![]() $\varphi , \psi \in {BMO}(\mathbb {R})$
. To see this, note that if
$\varphi , \psi \in {BMO}(\mathbb {R})$
. To see this, note that if
![]() $\varphi $
is nonzero on a set of positive measure, for some Lebesgue point of
$\varphi $
is nonzero on a set of positive measure, for some Lebesgue point of
![]() $\varphi $
like x,
$\varphi $
like x,
![]() $\varphi (x)\ne 0$
. Then, from the Lebesgue differentiation theorem, for sufficiently small
$\varphi (x)\ne 0$
. Then, from the Lebesgue differentiation theorem, for sufficiently small
![]() $\delta $
, we must have
$\delta $
, we must have
. So
![]() $\psi $
has bounded mean oscillation on intervals with length less than
$\psi $
has bounded mean oscillation on intervals with length less than
![]() $\delta $
. For intervals J with
$\delta $
. For intervals J with
![]() $l(J)\ge \delta $
,
$l(J)\ge \delta $
,
![]() $|\psi |$
has bounded averages because otherwise there is a sequence of intervals
$|\psi |$
has bounded averages because otherwise there is a sequence of intervals
![]() $J_n$
with
$J_n$
with
![]() $l(J_n)\ge \delta $
and
$l(J_n)\ge \delta $
and
. Then, by dividing each of these intervals into sufficiently small pieces of length between
![]() $\frac {\delta }{2}$
and
$\frac {\delta }{2}$
and
![]() $\delta $
, we conclude that
$\delta $
, we conclude that
![]() $|\psi |$
has large averages over such intervals, so
$|\psi |$
has large averages over such intervals, so
. But then,
![]() $\sup _{l(I)=\delta }O(\varphi ,I)=0$
, which means that
$\sup _{l(I)=\delta }O(\varphi ,I)=0$
, which means that
![]() $\varphi $
is constant. We summarize the above discussion in the following proposition.
$\varphi $
is constant. We summarize the above discussion in the following proposition.
Proposition 4.2 Let
![]() $f(x,y)=\varphi (x)\psi (y)$
,
$f(x,y)=\varphi (x)\psi (y)$
,
![]() $f\in {BMO}(\mathbb {R}^2)$
if and only if (11) holds and if
$f\in {BMO}(\mathbb {R}^2)$
if and only if (11) holds and if
![]() $f\ne 0$
, then
$f\ne 0$
, then
![]() $\varphi , \psi \in {BMO}(\mathbb {R})$
.
$\varphi , \psi \in {BMO}(\mathbb {R})$
.
Remark 4.3 When
![]() $\varphi $
and
$\varphi $
and
![]() $\psi $
are not constants, the above argument shows that they belong to
$\psi $
are not constants, the above argument shows that they belong to
![]() $bmo(\mathbb {R})$
, the nonhomogeneous
$bmo(\mathbb {R})$
, the nonhomogeneous
![]() $BMO$
space, which is a proper subspace of
$BMO$
space, which is a proper subspace of
![]() ${BMO}(\mathbb {R})$
. See [Reference Goldberg6] for more on
${BMO}(\mathbb {R})$
. See [Reference Goldberg6] for more on
![]() $bmo(\mathbb {R})$
.
$bmo(\mathbb {R})$
.
Corollary 4.4 Let
![]() $\log ^-|x|=\max \{0, -\log |x|\}$
be the negative part of the logarithm and
$\log ^-|x|=\max \{0, -\log |x|\}$
be the negative part of the logarithm and
![]() $p,q>0$
with
$p,q>0$
with
![]() $p+q\le 1$
. Then the function
$p+q\le 1$
. Then the function
![]() $f(x,y)=\left (\log ^-|x|\right )^p\left (\log ^-|y|\right )^q$
is in
$f(x,y)=\left (\log ^-|x|\right )^p\left (\log ^-|y|\right )^q$
is in
![]() ${BMO}(\mathbb {R}^2)$
.
${BMO}(\mathbb {R}^2)$
.
Remark 4.5 The above function f does not have bounded mean oscillation on rectangles, simply because the
![]() $BMO$
-norm of the slices becomes larger and larger as we get closer to the origin. See [Reference Korenovskii9, Example 2.32] for another example.
$BMO$
-norm of the slices becomes larger and larger as we get closer to the origin. See [Reference Korenovskii9, Example 2.32] for another example.
Now, we answer the third question of this paper.
Theorem 4.6 There exists a sequence of bounded functions
![]() $\{G_N\}$
,
$\{G_N\}$
,
![]() $N\ge 1$
such that it is bounded in
$N\ge 1$
such that it is bounded in
![]() ${BMO}(\mathbb {R}^2)$
but
${BMO}(\mathbb {R}^2)$
but
To prove this, we need the following simple lemma.
Lemma 4.7 Let
![]() $Q_0=[-1,1]^n$
, let
$Q_0=[-1,1]^n$
, let
![]() $f\in {BMO}(\mathbb {R}^n)$
with support in
$f\in {BMO}(\mathbb {R}^n)$
with support in
![]() $Q_0$
, and let
$Q_0$
, and let
![]() $x_k$
be a sequence in
$x_k$
be a sequence in
![]() $\mathbb {R}^n$
with
$\mathbb {R}^n$
with
![]() $|x_k-x_m|\ge 3\sqrt {n}$
for
$|x_k-x_m|\ge 3\sqrt {n}$
for
![]() $k\ne m$
. Then
$k\ne m$
. Then
![]() $g(x)=\sum f(x-x_k)$
is in
$g(x)=\sum f(x-x_k)$
is in
![]() ${BMO}(\mathbb {R}^n)$
and
${BMO}(\mathbb {R}^n)$
and
![]() $\|g\|_{{BMO}(\mathbb {R}^n)}\lesssim \|f\|_{{BMO}(\mathbb {R}^n)}$
.
$\|g\|_{{BMO}(\mathbb {R}^n)}\lesssim \|f\|_{{BMO}(\mathbb {R}^n)}$
.
Proof First, by comparing the average of
![]() $|f|$
on
$|f|$
on
![]() $Q_0$
with
$Q_0$
with
![]() $Q_0+2e_1$
, we have
$Q_0+2e_1$
, we have
Next, take a cube Q and suppose for some k,
![]() $Q\cap (x_k+Q_0)\ne \emptyset $
. We note that the distance of the support of functions
$Q\cap (x_k+Q_0)\ne \emptyset $
. We note that the distance of the support of functions
![]() $f(\cdot -x_k)$
from each other is at least
$f(\cdot -x_k)$
from each other is at least
![]() $\sqrt {n}$
, so if
$\sqrt {n}$
, so if
![]() $l(Q)\le 1$
, then
$l(Q)\le 1$
, then
![]() $O(g,Q)=O(f(\cdot -x_k),Q)\le \|f\|_{{BMO}(\mathbb {R}^n)}$
. Otherwise, we have
$O(g,Q)=O(f(\cdot -x_k),Q)\le \|f\|_{{BMO}(\mathbb {R}^n)}$
. Otherwise, we have

Now, to finish the proof, note that
![]() $\#\{k| Q\cap (x_k+Q_0)\ne \emptyset \}\lesssim |Q|$
, which implies
$\#\{k| Q\cap (x_k+Q_0)\ne \emptyset \}\lesssim |Q|$
, which implies
![]() $O(g,Q)\lesssim \|f\|_{{BMO}(\mathbb {R}^n)}$
.
$O(g,Q)\lesssim \|f\|_{{BMO}(\mathbb {R}^n)}$
.
Proof of Theorem 4.6
We may assume
![]() $n=2$
, since by a lifting argument similar to (6), we can conclude the theorem for higher dimensions. Let f be as in Corollary 4.4, let N be a positive integer, and consider the following function:
$n=2$
, since by a lifting argument similar to (6), we can conclude the theorem for higher dimensions. Let f be as in Corollary 4.4, let N be a positive integer, and consider the following function:
 $$ \begin{align*} g_N(x,y)=\sum_{k=0}^{N}\sum_{m=2^k}^{2^{k+1}-1}f\left(x-3\sqrt{2}m,y-\frac{k}{N}\right). \end{align*} $$
$$ \begin{align*} g_N(x,y)=\sum_{k=0}^{N}\sum_{m=2^k}^{2^{k+1}-1}f\left(x-3\sqrt{2}m,y-\frac{k}{N}\right). \end{align*} $$
![]() $g_N$
has the following properties:
$g_N$
has the following properties:
(i)
![]() $\|g_N\|_{{{BMO}(\mathbb {R}^2)}}\lesssim 1$
(here our bounds only depend on
$\|g_N\|_{{{BMO}(\mathbb {R}^2)}}\lesssim 1$
(here our bounds only depend on
![]() $p,q$
but not N).
$p,q$
but not N).
This follows from Corollary 4.4 and Lemma 4.7 applied to f with
![]() $x_{m,k}=\left (3\sqrt {2}m,\frac {k}{N}\right )$
.
$x_{m,k}=\left (3\sqrt {2}m,\frac {k}{N}\right )$
.
(ii)
![]() $M_s(g_N)(x,y) \ge M_{e_1}(g_N)(x,y)\gtrsim \left (\log N\right )^q$
for
$M_s(g_N)(x,y) \ge M_{e_1}(g_N)(x,y)\gtrsim \left (\log N\right )^q$
for
![]() $0\le x, y \le 1$
and
$0\le x, y \le 1$
and
![]() $N\ge 2$
.
$N\ge 2$
.
To see this, let
![]() $0\le x\le 1$
and
$0\le x\le 1$
and
![]() $\frac {l}{N}\le y <\frac {l+1}{N}$
for some
$\frac {l}{N}\le y <\frac {l+1}{N}$
for some
![]() $l<N$
. Then consider the average of
$l<N$
. Then consider the average of
![]() $(g_N)_y$
on
$(g_N)_y$
on
![]() $I=[0,3\cdot 2^{l+1}\sqrt {2}]$
, which is bounded from below by
$I=[0,3\cdot 2^{l+1}\sqrt {2}]$
, which is bounded from below by

Now, note that for
![]() $2^l\le m \le 2^{l+1}-1$
, I contains the support of
$2^l\le m \le 2^{l+1}-1$
, I contains the support of
![]() $f\left (\cdot -3\sqrt {2}m,y-\frac {l}{N}\right )$
, and since
$f\left (\cdot -3\sqrt {2}m,y-\frac {l}{N}\right )$
, and since
![]() $0\le y-\frac {l}{N}\le \frac {1}{N}$
, we have
$0\le y-\frac {l}{N}\le \frac {1}{N}$
, we have
From this, we get

At the end, we note that for every function g,
![]() $M_{e_1}(g)\le M_s(g)$
holds almost everywhere, and this proves the claim.
$M_{e_1}(g)\le M_s(g)$
holds almost everywhere, and this proves the claim.
(iii)
![]() $M_{e_1}(g_N)(x,y)=0$
for
$M_{e_1}(g_N)(x,y)=0$
for
![]() $y<-1$
.
$y<-1$
.
This holds simply because
![]() $g_N$
is supported in
$g_N$
is supported in
![]() $[3\sqrt {2}-1,\infty )\times [-1,2]$
.
$[3\sqrt {2}-1,\infty )\times [-1,2]$
.
(iv)
![]() $M_s(g_N)(x,y)\lesssim 1$
for
$M_s(g_N)(x,y)\lesssim 1$
for
![]() $0\le x\le 1, y\le -2$
.
$0\le x\le 1, y\le -2$
.
To prove this final property of
![]() $g_N$
, suppose
$g_N$
, suppose
![]() $ R=I\times J$
is a rectangle with
$ R=I\times J$
is a rectangle with
![]() $(x,y)\in R$
. Then, if
$(x,y)\in R$
. Then, if
![]() $R\cap {\mathrm{supp}}(g_N)\ne \emptyset $
, we have
$R\cap {\mathrm{supp}}(g_N)\ne \emptyset $
, we have
![]() $l(I),l(J)\ge 1$
, and we note that
$l(I),l(J)\ge 1$
, and we note that
which implies
Now, taking the supremum over all rectangles R proves the last property of
![]() $g_N$
.
$g_N$
.
Next, we measure the mean oscillation of
![]() $M_{e_1}(g_N)$
on the square
$M_{e_1}(g_N)$
on the square
![]() $[-3,3]^2$
by
$[-3,3]^2$
by
Then, from the second and third properties of
![]() $g_N$
, we obtain
$g_N$
, we obtain
and the same is true for
![]() $M_s$
by the third and fourth properties of
$M_s$
by the third and fourth properties of
![]() $g_N$
.
$g_N$
.
At this point, we note that the constructed sequence of functions
![]() $\{g_N\}$
has all the desired properties claimed in the theorem except that they are not bounded functions. However, this can be fixed by using a truncation argument as follows. For each
$\{g_N\}$
has all the desired properties claimed in the theorem except that they are not bounded functions. However, this can be fixed by using a truncation argument as follows. For each
![]() $N,M\ge 1$
, let
$N,M\ge 1$
, let
![]() $g_{N,M}$
be the truncation of
$g_{N,M}$
be the truncation of
![]() $g_N$
at height M, i.e.,
$g_N$
at height M, i.e.,
Next, we note that by the first property of
![]() $\{g_N\}$
, this sequence is bounded in
$\{g_N\}$
, this sequence is bounded in
![]() ${BMO}(\mathbb {R}^2)$
, and since
${BMO}(\mathbb {R}^2)$
, and since
![]() $\|g_{N,M}\|_{{{BMO}(\mathbb {R}^2)}}\le 4\|g_N\|_{{{BMO}(\mathbb {R}^2)}}$
, the double sequence
$\|g_{N,M}\|_{{{BMO}(\mathbb {R}^2)}}\le 4\|g_N\|_{{{BMO}(\mathbb {R}^2)}}$
, the double sequence
![]() $\left \{g_{N,M}\right \}$
is also bounded in
$\left \{g_{N,M}\right \}$
is also bounded in
![]() ${BMO}(\mathbb {R}^2)$
. Now, for each
${BMO}(\mathbb {R}^2)$
. Now, for each
![]() $N\ge 1$
,
$N\ge 1$
,
![]() $g_N$
is a compactly supported function in
$g_N$
is a compactly supported function in
![]() $L^2(\mathbb {R}^2)$
and the sequence
$L^2(\mathbb {R}^2)$
and the sequence
![]() $\left \{g_{N,M}\right \}$
converges to
$\left \{g_{N,M}\right \}$
converges to
![]() $g_N$
in
$g_N$
in
![]() $L^2(\mathbb {R}^2)$
as M goes to infinity. Then, since the operators
$L^2(\mathbb {R}^2)$
as M goes to infinity. Then, since the operators
![]() $M_{e_1}$
and
$M_{e_1}$
and
![]() $M_s$
are continuous on this space, we conclude that for each
$M_s$
are continuous on this space, we conclude that for each
![]() $N\ge 1$
,
$N\ge 1$
,
![]() $\left \{M_{e_1}(g_{N,M})\right \}$
and
$\left \{M_{e_1}(g_{N,M})\right \}$
and
![]() $\left \{M_s(g_{N,M})\right \}$
converge in
$\left \{M_s(g_{N,M})\right \}$
converge in
![]() $L^2(\mathbb {R}^2)$
to
$L^2(\mathbb {R}^2)$
to
![]() $M_{e_1}(g_N)$
and
$M_{e_1}(g_N)$
and
![]() $M_s(g_N)$
, respectively. Therefore, for
$M_s(g_N)$
, respectively. Therefore, for
![]() $N'$
large enough (depending on N), we have
$N'$
large enough (depending on N), we have
and
To finish the proof, let
![]() $G_N:=g_{N,N'}$
and note that
$G_N:=g_{N,N'}$
and note that
![]() $\left \{G_N\right \}$
is a sequence of bounded functions such that it is bounded in
$\left \{G_N\right \}$
is a sequence of bounded functions such that it is bounded in
![]() ${BMO}(\mathbb {R}^2)$
but
${BMO}(\mathbb {R}^2)$
but
By modifying the above function, one can construct a function in
![]() ${BMO}(\mathbb {R}^2)$
such that none of its horizontal slices are in
${BMO}(\mathbb {R}^2)$
such that none of its horizontal slices are in
![]() ${BMO}(\mathbb {R})$
, which provides a negative answer to the forth question of this paper.
${BMO}(\mathbb {R})$
, which provides a negative answer to the forth question of this paper.
Example Let
![]() $\{r_m\}$
be an enumeration of the rational numbers, and consider the following function:
$\{r_m\}$
be an enumeration of the rational numbers, and consider the following function:
Then we have
So, by density of the rational numbers, for all values of y, we get
![]() $\sup _{l(I)=2} O(h_y,I)=\infty $
, even though
$\sup _{l(I)=2} O(h_y,I)=\infty $
, even though
![]() $h\in {BMO}(\mathbb {R}^2)$
.
$h\in {BMO}(\mathbb {R}^2)$
.
The above example shows that one cannot control the maximum mean oscillation of the slices, when we look at intervals with a fixed length. However, in the following theorem, we show that there is a loose control when the length of intervals increases.
Theorem 4.8 Let
![]() $f\in {BMO}(\mathbb {R}^2)$
with
$f\in {BMO}(\mathbb {R}^2)$
with
![]() $\|f\|_{{{BMO}(\mathbb {R}^2)}}=1$
. Then there exist constants
$\|f\|_{{{BMO}(\mathbb {R}^2)}}=1$
. Then there exist constants
![]() $\lambda ,c>0$
, independent of f, such that for any sequence of intervals
$\lambda ,c>0$
, independent of f, such that for any sequence of intervals
![]() $I_k (k\ge 1$
) with
$I_k (k\ge 1$
) with
![]() $l(I_k)=2^k$
, and any interval J with
$l(I_k)=2^k$
, and any interval J with
![]() $l(J)=1$
, we have
$l(J)=1$
, we have
Proof Let
 $E_t=\left \{y\in J|\sup \limits _{k\ge 1}\frac {O\left (f_y,I_k\right )}{k}>t\right \}$
; then,
$E_t=\left \{y\in J|\sup \limits _{k\ge 1}\frac {O\left (f_y,I_k\right )}{k}>t\right \}$
; then,
 $$ \begin{align} E_t=\bigcup_{k\ge1} E_{t,k},\quad \quad E_{t,k}=\left\{y\in J| \frac{O\left(f_y,I_k\right)}{k}> t\right\}. \end{align} $$
$$ \begin{align} E_t=\bigcup_{k\ge1} E_{t,k},\quad \quad E_{t,k}=\left\{y\in J| \frac{O\left(f_y,I_k\right)}{k}> t\right\}. \end{align} $$
Now, taking the average over
![]() $E_{t,k}$
and applying Lemma 4.1 give us
$E_{t,k}$
and applying Lemma 4.1 give us
Next, let
![]() $J_k$
be the interval with the same center as J and with
$J_k$
be the interval with the same center as J and with
![]() $l(J_k)=2^k$
, and note that
$l(J_k)=2^k$
, and note that
![]() $E_{t,k}\subset J\subset J_k$
, so
$E_{t,k}\subset J\subset J_k$
, so
![]() $I_k\times E_{t,k}\subset I_k\times J_k$
. Then an application of Lemma 3.2 shows that
$I_k\times E_{t,k}\subset I_k\times J_k$
. Then an application of Lemma 3.2 shows that
 $$\begin{align*}t\lesssim \frac{1}{k}O\left(f,I_k\times E_{t,k}\right)\lesssim\frac{1}{k}\left(1+\log\frac{|I_k\times J_k|}{|I_k\times E_{t,k}|}\right)\lesssim 1-\frac{1}{k}\log|E_{t,k}|. \end{align*}$$
$$\begin{align*}t\lesssim \frac{1}{k}O\left(f,I_k\times E_{t,k}\right)\lesssim\frac{1}{k}\left(1+\log\frac{|I_k\times J_k|}{|I_k\times E_{t,k}|}\right)\lesssim 1-\frac{1}{k}\log|E_{t,k}|. \end{align*}$$
So, for an appropriate constant
![]() $a>0$
, which is independent of f, we have
$a>0$
, which is independent of f, we have
![]() $|E_{t,k}|\lesssim e^{-atk}$
for
$|E_{t,k}|\lesssim e^{-atk}$
for
![]() $t>0$
. From this and (13), we get the estimate
$t>0$
. From this and (13), we get the estimate
Now, an application of Cavalieri’s principle gives us
Hence, (4.8) holds with
![]() $\lambda =\frac {a}{2}$
, and this finishes the proof.
$\lambda =\frac {a}{2}$
, and this finishes the proof.
Acknowledgment
I would like to thank G. Dafni and R. Gibara for suggesting these problems and valuable discussions and comments. Also, I am grateful to the referee for all the valuable comments on the manuscript.