Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-27T06:15:09.773Z Has data issue: false hasContentIssue false
  • English
  • Français

The Maximal Extension of a Zero-dimensional Product Space

Published online by Cambridge University Press:  20 November 2018

Haruto Ohta
Haruto Ohta*
Affiliation:
Faculty of Education, Shizuoka University, Ohya, Shizuoka, 422, Japan
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

It is known that if a topological property 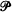of Tychonoff spaces is closed-hereditary, productive and possessed by all compact Hausdorff spaces, then each (0-dimensional) Tychonoff space X is a dense subspace of a (0-dimensional) Tychonoff space 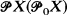with 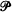such that each continuous map from X to a (0-dimensional) Tychonoff space with 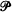admits a continuous extension over 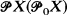. In response to Broverman's question [Canad. Math. Bull. 19 (1), (1976), 13–19], we prove that if for every two 0-dimensional Tychonoff spaces X and Y, 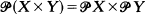if and only if 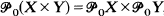, then 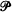is contained in countable compactness.

Keywords

Primary 54D3554B10Secondary 54B30Extension propertymaximal extension0-dimensional spaceproductcountably compactultrarealcompactPz(ℵ1)-compactStone-Čech compactification
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 26 , Issue 2 , 01 June 1983 , pp. 192 - 201
Copyright
Copyright © Canadian Mathematical Society 1983

References

1. Arhangel'skiǐ, A. V., Bicompact sets and the topology of spaces, Trudy Moscov. Mat. Obšč. 13 (1965), 3–55= Trans. Moscow Math. Soc. 13 (1965), 1–62.Google Scholar
2. Banaschewski, B., Über nulldimensionale Raiime, Math. Nachr. 13 (1955), 129–140.Google Scholar
3. Broverman, S., The topological extension of a product, Canad. Math. Bull. 19 (1) (1976), 13–19.Google Scholar
4. Comfort, W. W., On the Hewitt realcompactification of a product space, Trans. Amer. Math. Soc. 131 (1968), 107–118.Google Scholar
5. Dowker, C. H., Local dimension of normal spaces, Quart. J. Math. Oxford (2), 6 (1955), 101–120.Google Scholar
6. Engelking, R., General Topology, Polish Scientific Publishers, Warszawa, 1977.Google Scholar
7. Engelking, R. and Mrόwka, S., On E-compact spaces, Bull. Acad. Polon. Sci. Sér. Math. 6 (1958), 429–436.Google Scholar
8. Herrlich, H. and van der Slot, J., Properties which are closely related to compactness, Indag. Math. 29 (1967), 524–529.Google Scholar
9. Isbell, J. R., Uniform spaces, Math. Surveys, no. 12, Amer. Math. Soc, Providence, R.I., 1964.Google Scholar
10. Kuratowski, K., Topology I, II, Academic Press, New York, 1966.Google Scholar
11. Mrόwka, S., On E-compact spaces II, Bull. Acad. Polon. Sci. Sér. Math. 14 (1966), 597–605.Google Scholar
12. Ohta, H., The Hewitt realcompactification of products, Trans. Amer. Math. Soc. 263 (1981), 363–375.Google Scholar
13. Ohta, H., Topological extension properties and projective covers, to appear in Canad. J. Math. Google Scholar
14. Pears, A. R., Dimension theory of general spaces, Cambridge Univ. Press, Cambridge, 1975.Google Scholar
15. Terada, T., New topological extension properties, Proc. Amer. Math. Soc. 67 (1977), 162-166.Google Scholar
16. Woods, R. G., Topological extension properties, Trans. Amer. Math. Soc. 210 (1975), 365-385.Google Scholar