Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-27T13:17:15.687Z Has data issue: false hasContentIssue false
  • English
  • Français

$L$-Series of Certain Elliptic Surfaces

Published online by Cambridge University Press:  20 November 2018

Ling Long
Ling Long*
Affiliation:
Department of Mathematics The Pennsylvania State University University Park, Pennsylvania 16802 USA
*
Current address: Department of Mathematics Iowa State University Ames, IA 50011 USA
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

In this paper, we study the modularity of certain elliptic surfaces by determining their 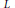$L$-series through their monodromy groups.

Keywords

14J2711M06
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 46 , Issue 4 , 01 December 2003 , pp. 546 - 558
Copyright
Copyright © Canadian Mathematical Society 2003

References

[AO00] Ahlgren, S. and Ono, K., Modularity of a certain Calabi-Yau threefold. Monatsh.Math. (3) 129 (2000), 177–190.Google Scholar
[Del73] Deligne, P., Formes modulaires et représentations de gl(2). In: Modular functions of one variable, II (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Math 349, Springer, Berlin, 1973, 55–105.Google Scholar
[Dwo60] Dwork, B., On the rationality of the zeta function of an algebraic variety. Amer. J. Math. 82 (1960), 631–648.Google Scholar
[Eva81] Evans, R. J., Identities for products of Gauss sums over finite fields. Enseign.Math. (2) 27(1981), (3-4)(1982), 197–209.Google Scholar
[Kod63] Kodaira, K., On compact analytic surfaces. II, III. Ann. of Math. (2) 77 (1963), 563–626, ibid. 78 (1963), 1–40.Google Scholar
[Lan62] Lang, S., Diophantine geometry. Interscience Publishers (a division of John Wiley & Sons), New York, London, 1962.Google Scholar
[Li96] Winnie Li, W. C., Number theory with applications. World Scientific Publishing Co. Inc., River Edge, NJ, 1996.Google Scholar
[Liv87] Livné, R., Cubic exponential sums and Galois representations. In: Current trends in arithmetical algebraic geometry (Arcata, Calif., 1985), Contemp.Math. 67, Amer.Math. Soc., Providence, RI, 1987, 247–261.Google Scholar
[Lon03] Long, L., The Shioda-Inose structure of one-parameter families of K3 surfaces. Preprint, 2003.Google Scholar
[Nér64] Néron, A., Modèles minimaux des variétés abéliennes sur les corps locaux et globaux. Inst. Hautes E´ tudes Sci. Publ. Math. 21(1964), 128.Google Scholar
[Nor85] Nori, M., On certain elliptic surfaces with maximal Picard number. Topology (2) 24 (1985), 175–186.Google Scholar
[SB85] Stienstra, J. and Beukers, F., On the Picard-Fuchs equation and the formal Brauer group of certain elliptic K3-surfaces. Math. Ann. (2) 271 (1985), 269–304.Google Scholar
[Seb01] Sebbar, A., Classification of torsion-free genus zero congruence groups. Proc. Amer. Math. Soc. (9) 129 (2001), 2517–2527 (electronic).Google Scholar
[Shi71] Shimura, G., Introduction to the arithmetic theory of automorphic functions. Publications of the Math. Society of Japan 11, Iwanami Shoten, Publishers, Tokyo, 1971, Kan .o Memorial Lectures 1.Google Scholar
[Shi72] Shioda, T., On elliptic modular surfaces. J. Math. Soc. Japan 24 (1972), 20–59.Google Scholar
[SI77] Shioda, T. and Inose, H., On singular K3 surfaces. In: Complex analysis and algebraic geometry, Iwanami Shoten, Tokyo, 1977, 119–136.Google Scholar
[Tat75] Tate, J., Algorithm for determining the type of a singular fiber in an elliptic pencil. In: Modular functions of one variable, IV (Proc. Internat. Summer School, Univ. Antwerp, Antwerp, 1972), Lecture Notes in Math. 476, Springer, Berlin, 1975, 33–52.Google Scholar
[Ver00] Verrill, H. A., The L-series of certain rigid Calabi-Yau threefolds. J. Number Theory (2) 81 (2000), 310–334.Google Scholar
[Yui01] Yui, N., Arithmetic of certain Calabi-Yau varieties and mirror symmetry. In: Arithmetic algebraic geometry (Park City, UT, 1999), IAS/Park City Math. Ser. 9, Amer. Math. Soc., Providence, RI, 2001, 507–569.Google Scholar