Hostname: page-component-586b7cd67f-rcrh6 Total loading time: 0 Render date: 2024-11-24T08:25:12.729Z Has data issue: false hasContentIssue false
  • English
  • Français

Local Malcev Conditions

Published online by Cambridge University Press:  20 November 2018

Alden F. Pixley
Alden F. Pixley*
Affiliation:
Harvey Mudd College, the Claremont Colleges, Claremont, California
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

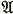Let p and q be polynomial symbols of a type of algebras having operations ∨, ∧, and; (interpreted as the join, meet, and product of congruence relations). If is an algebra, L(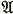), the local variety of 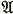, is the class of all algebras 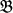such that for each finite subset G of 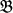there is a finite subset F of 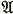such that every identity of F is also an identity of G.

THEOREM. There is an algorithm which, for each inequality

p≤q,

and pair of integers n, k≥2, determines a set Un, k of (Malcev) equations with the property:

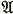For each algebra, p≤q is true in the congruence lattice of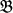for each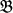∊L(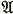) if and only if for each finite subset F of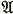and integer n≥2 there is a k=k(n, F) such that Un, kare identities of F.

This generalizes a corresponding result for varieties due to Wille (Kongruenzklassengeometrien, Lect. Notes in Math. Springer- Verlag, Berlin-Heidelberg, New York, 1970) and at the same time provides a more direct proof.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 4 , December 1972 , pp. 559 - 568
Copyright
Copyright © Canadian Mathematical Society 1972

References

1. Day, A., A characterization of modularity for congruence lattices of algebras, Canad. Math. Bull. 12(1969), 167-173.Google Scholar
2. Foster, A. L., Functional completeness in the small. Algebraic cluster theorems and identities, Math. Ann. 143(1961), 29-58.Google Scholar
3. Grätzer, G., Two Malcev type theorems in universal algebra, J. Comb. Theory. 8 (1970), 334-342.Google Scholar
4. Tah-Kai, Hu, On the fundamental subdirect factorization theorems of primal algebra theory, Math. Z. 112(1969), 154-162.Google Scholar
5. Tah-Kai, Hu and Philip, Kelenson, Independence and direct factorization of universal algebras, Math. Nachr. 51 (1971), 83-99.Google Scholar
6. Jónsson, B., Algebras whose congruence lattices are distributive, Math. Scand. 21 (1967), 110-121.Google Scholar
7. Malcev, A. I., On the general theory of algebraic systems, Mat. Sb. (77) 35 (1954), 3-20.Google Scholar
8. Pixley, A. F., Distributivity and permutability of congruences in equational classes, Proc. Amer. Math. Soc. 14 (1963), 105-109.Google Scholar
9. Pixley, A. F., 9 The ternary discriminator function in universal algebra, Math. Ann. 191 (1971), 167-180.Google Scholar
10. Wille, R., Kongruenzklassengeometrien, Lecture Notes in Math. 113, Springer-Verlag, Berlin-Heidelberg-New York, 1970.Google Scholar