Hostname: page-component-6587cd75c8-ptrpl Total loading time: 0 Render date: 2025-04-23T23:54:37.004Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear fractional self-maps of the unit ball

Part of: Holomorphic functions of several complex variables Special classes of linear operators

Published online by Cambridge University Press:  15 November 2023

Michael R. Pilla Open the ORCID record for Michael R. Pilla [Opens in a new window]
Michael R. Pilla*
Affiliation:
Department of Mathematical Sciences, Ball State University, Muncie, IN 47306, United States
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

Determining the range of complex maps plays a fundamental role in the study of several complex variables and operator theory. In particular, one is often interested in determining when a given holomorphic function is a self-map of the unit ball. In this paper, we discuss a class of maps in 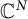$\mathbb {C}^N$ that generalize linear fractional maps. We then proceed to determine precisely when such a map is a self-map of the unit ball. In particular, we take a novel approach, obtaining numerous new results about this class of maps along the way.

Keywords

Linear fractional mapsunit ballself-maps

MSC classification

Primary: 32A10: Holomorphic functions
Secondary: 32A40: Boundary behavior of holomorphic functions 47B50: Operators on spaces with an indefinite metric
Type
Article
Information
Canadian Mathematical Bulletin , Volume 67 , Issue 2 , June 2024 , pp. 458 - 468
Check for updates
Copyright
© The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Ahn, H., Byun, J., and Park, J.-D., Automorphisms of the Hartogs type domains over classical symmetric domains . Internat. J. Math. 23(2012), 1250098.CrossRefGoogle Scholar
Bisi, C. and Bracci, F., Linear fractional maps of the unit ball: A geometric study . Adv. Math. 167(2002), no. 2, 265–287.CrossRefGoogle Scholar
Cowen, C. and MacCluer, B., Linear fractional maps of the ball and Theiry composition operators . Acta Sci. Math. (Szeged) 66(2000), 351–376.Google Scholar
Humphreys, J., Linear algebraic groups, Graduate Texts in Mathematics, Springer, New York, 1981.Google Scholar
Hinkkanen, A., Schur products of certain polynomials, Lipa’s Legacy . Contemp. Math. 211(1998), 285–295.CrossRefGoogle Scholar
MacCluer, B., Iterates of holomorphic self-maps of the unit ball in ${\mathbb{C}}^N$ . Michigan Math. J. 30(1983), no. 1, 97–106.CrossRefGoogle Scholar
Martín, M., Composition operators with linear fractional symbols and their adjoints, First Advanced Course in Operator Theory and Complex Analysis, University of Seville, Seville, 2004.Google Scholar
Pilla, M. R., A generalized cross ratio. To appear. Preprint, 2021. arXiv:2106.10570 Google Scholar
Press, W., Flannery, B., Teukolsky, S., and Vetterling, W., Numerical recipes in Fortran 77: The art of scientific computing. 2nd ed., Cambridge University Press, Cambridge, 1992.Google Scholar
Richman, A., The range of linear fractional maps on the unit ball . Proc. Amer. Math. Soc. 131(2003), 889–895.CrossRefGoogle Scholar
Rudin, W., Function theory in polydiscs, Mathematics Lecture Note Series, 41, W.A. Benjamin, New York, 1969.Google Scholar
Rudin, W., Function theory in the unit ball of  ${\mathbb{C}}^n$ , Grundlehren der Mathematischen Wissenschaften [Fundamental Principles of Mathematical Science], 241, Springer, New York, 1980.CrossRefGoogle Scholar