Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-25T17:32:44.233Z Has data issue: false hasContentIssue false
  • English
  • Français

Linear Forms in Monic Integer Polynomials

Published online by Cambridge University Press:  20 November 2018

Artūras Dubickas
Artūras Dubickas*
Affiliation:
Department of Mathematics and Informatics, Vilnius University, Naugarduko 24, Vilnius LT-03225, Lithuania e-mail: [email protected] Institute of Mathematics and Informatics, Vilnius University, Akademijos 4, Vilnius LT-08663, Lithuania
Rights & Permissions [Opens in a new window]

Abstract.

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We prove a necessary and sufficient condition on the list of nonzero integers ${{u}_{1}},...,{{u}_{k}}$, 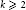$k\,\ge \,2$, under which a monic polynomial 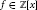$f\,\in \,\mathbb{Z}\left| x \right|$ is expressible by a linear form ${{u}_{1}}\,{{f}_{1}}\,+\,\cdot \cdot \cdot \,+\,{{u}_{k}}\,{{f}_{k}}$ in monic polynomials ${{f}_{1}},...,\,{{f}_{k}}\,\in \,\mathbb{Z}\left| x \right|$. This condition is independent of 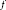$f$. We also show that if this condition holds, then the monic polynomials ${{f}_{1}},...,\,{{f}_{k}}$ can be chosen to be irreducible in 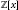$\mathbb{Z}\left[ x \right]$.

Keywords

11R0911C0811B83irreducible polynomialheightlinear form in polynomialsEisenstein's criterion.
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 56 , Issue 3 , 01 September 2013 , pp. 510 - 519
Copyright
Copyright © Canadian Mathematical Society 2013

References

[1] Betts, C., Additive and subtractive irreducible monic decompositions in Z[x]. C. R. Math. Acad. Sci. Soc. R. Can. 20 (1998), no. 3, 86–90.Google Scholar
[2] Dubickas, A., Polynomials expressible by sums of monic integer irreducible polynomials Bull. Math. Soc. Sci. Math. Roumanie 54 (102)(2011), no. 1, 65–81.Google Scholar
[3] Effinger, G.W. and Hayes, D. R., A complete solution to the polynomial 3-primes problem. Bull. Amer. Math. Soc. (N.S.) 24 (1991), no. 2, 363–369. http://dx.doi.org/10.1090/S0273-0979-1991-16035-0 Google Scholar
[4] Hayes, D. R., A Goldbach theorem for polynomials with integer coefficients. Amer. Mat h. Monthly, 72 (1965), 45–46. http://dx.doi.org/10.2307/2312999 Google Scholar
[5] Hayes, D. R., The expression of a polynomial as a sum of three irreducibles. Acta Arith. 11 (1966), 461–488.Google Scholar
[6] Kozek, M., An asymptotic formula for Goldbach's conjecture with monic polynomials. Amer. Math. Monthly 117 (2010), no. 4, 365–369. http://dx.doi.org/10.4169/000298910X480856 Google Scholar
[7] Pollack, P., On polynomial rings with a Goldbach property. Amer. Mat Monthly h., 118 (2011), no. 1, 71–77.Google Scholar
[8] Rattan, A. and Stewart, C., Goldbach's conjecture for Z[x]. C. R. Math. Acad. Sci. Soc. R. Can. 20 (1998)), no. 3, 83–85.Google Scholar
[9] Saidak, F., On Goldbach's conjecture for integer polynomials. Amer. Math. Monthly 113 (2006), no. 6, 541–545. http://dx.doi.org/10.2307/27641978 Google Scholar
[10] Schinzel, A., Polynomials with special regard to irreducibility. Encyclopedia of Mathematics and its Applications, 77, Cambridge University Press, Cambridge, 2000.Google Scholar
[11] Vaserstein, L. N., Noncommutative number theory. In: Algebraic K-theory and algebraic number theory (Honolulu, Haway, 1987), Contemp. Math., 83, American Mathematical Society, Providence, RI, 1989, pp. 445–449.Google Scholar
[12] Wang, J., Goldbach's problem in the ring Mn(Z), Amer. Math. Monthly 99 (1992), no. 9, 856–857. http://dx.doi.org/10.2307/2324122 Google Scholar
[13] Wang, S., The Goldbach 3-primes property for polynomial rings over certain infinite fields. Chinese Sci. Bull. 43 (1998), no. 15, 1256–1260. http://dx.doi.org/10.1007/BF02884136 Google Scholar