Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Khoshnevisan, Davar
and
Lewis, Thomas M.
1998.
A law of the iterated logarithm for stable processes in random scenery.
Stochastic Processes and their Applications,
Vol. 74,
Issue. 1,
p.
89.
Khoshnevisan, Davar
and
Lewis, Thomas M.
1999.
Stochastic calculus for Brownian motion on a Brownian fracture.
The Annals of Applied Probability,
Vol. 9,
Issue. 3,
Révész, Pál
and
Shi, Zhan
2000.
Strong approximation of spatial random walk in random scenery.
Stochastic Processes and their Applications,
Vol. 88,
Issue. 2,
p.
329.
Gu, Yu
and
Bal, Guillaume
2014.
An invariance principle for Brownian motion in random scenery.
Electronic Journal of Probability,
Vol. 19,
Issue. none,
Gu, Yu
and
Bal, Guillaume
2015.
Homogenization of parabolic equations with large time-dependent random potential.
Stochastic Processes and their Applications,
Vol. 125,
Issue. 1,
p.
91.
Gu, Yu
and
Bal, Guillaume
2016.
Weak convergence approach for parabolic equations with large, highly oscillatory, random potential.
Annales de l'Institut Henri Poincaré, Probabilités et Statistiques,
Vol. 52,
Issue. 1,


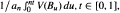 , where {B
, where {B