Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-26T13:47:18.298Z Has data issue: false hasContentIssue false
  • English
  • Français

Lie Derivatives and Ricci Tensor on Real Hypersurfaces in Complex Two-plane Grassmannians

Published online by Cambridge University Press:  20 November 2018

Imsoon Jeong ,
Juan de Dios Pérez ,
Young Jin Suh  and
Changhwa Woo
Imsoon Jeong
Affiliation:
Division of Future Capability Education, Ju Si-Gyeong College, Pai Chai University, 155-40 Baejae-ro, Seo-gu, Daejeon, 35345, Republic of Korea, e-mail : [email protected]
Juan de Dios Pérez
Affiliation:
Departamento de Geometria y Topologia, Universidad de Granada, 18071-Granada, Spain, e-mail : [email protected]
Young Jin Suh
Affiliation:
Department of Mathematics and Research Institute of Real and Complex Manifold, Kyungpook National University, Daegu 41566, Republic of Korea, e-mail : [email protected]
Changhwa Woo
Affiliation:
Department of Mathematics Education, Woosuk University, 565-701 Wanju, Jeonbuk, Republic Of Korea, e-mail : [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

On a real hypersurface 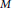$M$ in a complex two-plane Grassmannian ${{G}_{2}}\left( {{\mathbb{C}}^{m+2}} \right)$ we have the Lie derivation 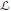$\mathcal{L}$ and a differential operator of order one associated with the generalized Tanaka–Webster connection 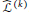${{\widehat{\mathcal{L}}}^{\left( k \right)}}$. 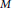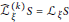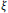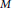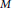We give a classification of real hypersurfaces $M$ on ${{G}_{2}}\left( {{\mathbb{C}}^{m+2}} \right)$ satisfying $\widehat{\mathcal{L}}_{\xi }^{\left( k \right)}\,S\,=\,{{\mathcal{L}}_{\xi }}S$, where $\xi$ is the Reeb vector field on $M$ and $s$ the Ricci tensor of $M$.

Keywords

53C4053C15real hypersurfacecomplex two-plane GrassmannianHopf hypersurfaceshape operatorRicci tensorLie derivation
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 61 , Issue 3 , 01 September 2018 , pp. 543 - 552
Copyright
Copyright © Canadian Mathematical Society 2018

References

[1] Cho, J. T., CR structures on real hypersurfaces of a complex Space form. Publ. Math. Debrecen 54(1999), no. 3-4, 473–487.Google Scholar
[2] Cho, J. T., Levi parallel hypersurfaces in a complex Space form. Tsukuba J. Math. 30 (2006), no. 2, 329–343. http://dx.doi.Org/10.21099/tkbjm/1496165066Google Scholar
[3] Hörn, R. A. and Johnson, C. R., Matrix analysis. Cambridge University Press, Cambridge, 1985. http://dx.doi.Org/10.1017/CBO9780511810817Google Scholar
[4] Jeong, I., Machado, C., Perez, J. D., and Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with D1-parallel structure facobi Operator. Internat. J. Math. 22 (2011), no. 5, 655–673. http://dx.doi.org/!0.1142/S0129167X11 006957Google Scholar
[5] Lee, H., Choi, Y. S., and Woo, C., Hopf hypersurfaces in complex two-plane Grassmannians with Reeb parallel shape Operator. Bull. Malays. Math. Sei. Soc. 38 (2015), no. 2, 617–634. http://dx.doi.Org/10.1007/s40840-014-0039-3Google Scholar
[6] Lee, H. and Suh, Y. J., Real hypersurfaces oftype B in complex two-plane Grassmannians related to the Reeb vector. Bull. Korean Math. Soc. 47 (2010), no. 3, 551–561. http://dx.doi.Org/10.4134/BKMS.2010.47.3.551Google Scholar
[7] Loo, T. H., Semi-parallel real hypersurfaces in complex two-plane Grassmannians. Differential Geom. Appl. 34(2014), 87–102. http://dx.doi.Org/10.1016/j.difgeo.2014.03.011Google Scholar
[8] Pak, E., Suh, Y. J., and Woo, C., Restricted Ricci conditions for real hypersurfaces in complex two-plane Grassmannians. Houston J. Math. 41 (2015), no. 3, 767–783.Google Scholar
[9] Perez, J. D., Jeong, I., and Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with commuting normal Jacobi Operator. ActaMath. Hungar. 117(2007), 201–217. http://dx.doi.org/10.1007/s10474-007-6091-9Google Scholar
[10] Perez, J. D. and Suh, Y. J., The Ricci tensor ofreal hypersurfaces in complex two-plane Grassmannians. J. Korean Math. Soc. 44(2007), 211–235. http://dx.doi.Org/10.4134/JKMS.2007.44.1.211Google Scholar
[11] Perez, J. D., Suh, Y. J., and Watanabe, Y., Generalized Einstein real hypersurfaces in complex two-plane Grassmannians. J. Geom. Phys. 60(2010), 1806–1818. http://dx.doi.Org/10.1016/j.geomphys.2010.06.01 7Google Scholar
[12] Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with commuting Ricci tensor. J. Geom. Phys. 60(2010), 1792–1805. http://dx.doi.Org/10.1016/j.geomphys.2010.06.007Google Scholar
[13] Suh, Y. J., Real hypersurfaces in complex two-plane Grassmannians with parallel Ricci tensor. Proc. Roy. Soc. Edinburgh Sect. A. 142(2012), 1309–1324. http://dx.doi.org/10.1017/S0308210510001472Google Scholar
[14] Suh, Y. J., Real hypersurfaces in the complex quadric with parallel Ricci tensor. Adv. Math. 281(2015), 886–905. http://dx.doi.Org/10.1016/j.aim.2015.05.012Google Scholar
[15] Suh, Y. J., Real hypersurfaces in the complex quadric with harmonic curvature. J. Math. Pures Appl. 106(2016), 393–410. http://dx.doi.Org/10.1016/j.matpur.2016.02.015Google Scholar
[16] Suh, Y. J. and Yang, H. Y., Real hypersurfaces in complex two-plane Grassmannians with commuting strueture Jacobi Operator. Bull. Korean Math. Soc. 45 (2008), no. 3, 495–507. http://dx.doi.Org/10.4134/BKMS.2008.45.3.495Google Scholar
[17] Tanaka, N., On non-degenerate real hypersurfaces, graded Lie algebras and Cartan connections. Japan. J. Math. (N.S.) 2(1976), 131–190.Google Scholar
[18] Tanno, S., Variationalproblems on contact Riemannian manifolds. Trans. Amer. Math. Soc. 314(1989), 349–379. http://dx.doi.org/10.1090/S0002-9947-1989-1000553-9Google Scholar
[19] Webster, S. M., Peudo-Hermitian struetures on a real hypersurface. J. Differential Geom. 13(1978), 25–41. http://dx.doi.Org/10.4310/jdg/1214434345Google Scholar