Hostname: page-component-cd9895bd7-dk4vv Total loading time: 0 Render date: 2024-12-25T19:23:25.693Z Has data issue: false hasContentIssue false
  • English
  • Français

Lie Derivations on Skew Elements in Prime Rings With Involution

Published online by Cambridge University Press:  20 November 2018

Eleanor Killam
Eleanor Killam*
Affiliation:
Department of Mathematics and Statistics University of Massachusetts Amherst, Massachusetts 01003
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let R be a prime ring with involution satisfying x/2 ∊ R whenever x ∊ R. Assume that R has two nontrivial symmetric idempotents e1, e2 whose sum is not 1, and that the subrings determined by e1, e2, 1 — (e1 + e2) are not orders in simple rings of dimension at most 4 over their centers. Then if L is a Lie derivation of the skew elements K into R there exists a subring A of R, A ⊆ 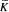, a derivation D :A → RC, the central closure of R, and a mapping T:R → C, satisfying L = D + T on K and = 0.

Keywords

16A72
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 30 , Issue 3 , 01 September 1987 , pp. 344 - 350
Copyright
Copyright © Canadian Mathematical Society 1987

References

1. Ericson, T.S., The Lie Structure in Prime Rings with Involution, J. Algebra 21 (1972), pp. 523 — 534.Google Scholar
2. Jacobs, D.R., Lie Derivations on the Skew Elements of Simple Rings with Involution, Ph.D. dissertation, University of Massachusetts, 1973.Google Scholar
3. W. S., Martindale III, Lie Derivations of Primitive Rings, Mich. Math. J. 11 (1964), pp. 183–187.Google Scholar