Article contents
Left orderable surgeries of double twist knots II
Published online by Cambridge University Press: 27 August 2020
Abstract
A slope r is called a left orderable slope of a knot
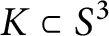 $K \subset S^3$
if the 3-manifold obtained by r-surgery along K has left orderable fundamental group. Consider double twist knots
$K \subset S^3$
if the 3-manifold obtained by r-surgery along K has left orderable fundamental group. Consider double twist knots
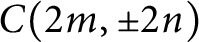 $C(2m, \pm 2n)$
and
$C(2m, \pm 2n)$
and
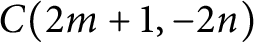 $C(2m+1, -2n)$
in the Conway notation, where
$C(2m+1, -2n)$
in the Conway notation, where
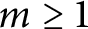 $m \ge 1$
and
$m \ge 1$
and
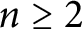 $n \ge 2$
are integers. By using continuous families of hyperbolic
$n \ge 2$
are integers. By using continuous families of hyperbolic
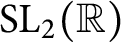 ${\mathrm {SL}}_2(\mathbb {R})$
-representations of knot groups, it was shown in [8, 16] that any slope in
${\mathrm {SL}}_2(\mathbb {R})$
-representations of knot groups, it was shown in [8, 16] that any slope in
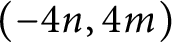 $(-4n, 4m)$
(resp.
$(-4n, 4m)$
(resp.
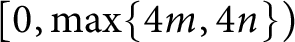 $ [0, \max \{4m, 4n\})$
) is a left orderable slope of
$ [0, \max \{4m, 4n\})$
) is a left orderable slope of
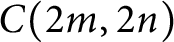 $C(2m, 2n)$
(resp.
$C(2m, 2n)$
(resp.
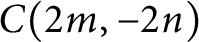 $C(2m, - 2n)$
) and in [6] that any slope in
$C(2m, - 2n)$
) and in [6] that any slope in
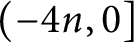 $(-4n,0]$
is a left orderable slope of
$(-4n,0]$
is a left orderable slope of
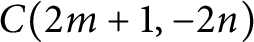 $C(2m+1,-2n)$
. However, the proofs of these results are incomplete, since the continuity of the families of representations was not proved. In this paper, we complete these proofs, and, moreover, we show that any slope in
$C(2m+1,-2n)$
. However, the proofs of these results are incomplete, since the continuity of the families of representations was not proved. In this paper, we complete these proofs, and, moreover, we show that any slope in
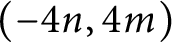 $(-4n, 4m)$
is a left orderable slope of
$(-4n, 4m)$
is a left orderable slope of
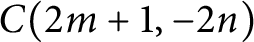 $C(2m+1,-2n)$
detected by hyperbolic
$C(2m+1,-2n)$
detected by hyperbolic
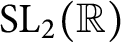 ${\mathrm {SL}}_2(\mathbb {R})$
-representations of the knot group.
${\mathrm {SL}}_2(\mathbb {R})$
-representations of the knot group.
MSC classification
- Type
- Article
- Information
- Copyright
- © Canadian Mathematical Society 2020
Footnotes
The first author has been partially supported by the Vietnam National Foundation for Science and Technology Development (NAFOSTED) under grant number 101.04-2015.20. The second author has been partially supported by JSPS KAKENHI Grant Number JP20K03587. The third author has been partially supported by a grant from the Simons Foundation (354595).
References
- 1
- Cited by



