Hostname: page-component-cd9895bd7-gxg78 Total loading time: 0 Render date: 2024-12-25T18:45:23.122Z Has data issue: false hasContentIssue false
  • English
  • Français

Lefschetz Numbers for C*-Algebras

Published online by Cambridge University Press:  20 November 2018

Heath Emerson
Heath Emerson*
Affiliation:
University of Victoria, Victoria, BCe-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Using Poincaré duality, we obtain a formula of Lefschetz type that computes the Lefschetz number of an endomorphism of a separable nuclear 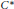${{C}^{*}}$-algebra satisfying Poincaré duality and the Kunneth theorem. (The Lefschetz number of an endomorphism is the graded trace of the induced map on $\text{K}$-theory tensored with $\mathbb{C}$, as in the classical case.) We then examine endomorphisms of Cuntz–Krieger algebras 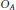${{O}_{A}}$. An endomorphism has an invariant, which is a permutation of an infinite set, and the contracting and expanding behavior of this permutation describes the Lefschetz number of the endomorphism. Using this description, we derive a closed polynomial formula for the Lefschetz number depending on the matrix A and the presentation of the endomorphism.

Keywords

19K3546L80
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 54 , Issue 1 , 01 March 2011 , pp. 82 - 99
Copyright
Copyright © Canadian Mathematical Society 2011

References

[1] Brodzki, J., Mathai, V., Rosenberg, J., and Szabo, R., D-branes, RR-fields and duality on noncommutative manifolds. Comm. Math. Phys. 277(2008), no. 3, 643–706. doi:10.1007/s00220-007-0396-yGoogle Scholar
[2] Cuntz, J., A class of C*-algebras and topological Markov chains. II. Reducible chains and the Ext-functor for C*-algebras. Invent. Math. 63(1981), no. 1, 25–40. doi:10.1007/BF01389192Google Scholar
[3] Cuntz, J. and Krieger, W., A class of C*-algebras and topological Markov chains. Invent. Math. 56(1980), no. 3, 251–268. doi:10.1007/BF01390048Google Scholar
[4] Connes, A., Noncommutative geometry. Academic Press Inc., San Diego, CA, 1994.Google Scholar
[5] Emerson, H., Noncommutative Poincaré duality for boundary actions of hyperbolic groups. J. Reine Angew. Math. 564(2003), 1–33. doi:10.1515/crll.2003.090Google Scholar
[6] Echterhoff, S., Emerson, H., and Kim, H.-J., A Lefschetz fixed-point formula for certain orbifold C*-algebras. J. Noncommut. Geom. 4(2010), no. 1, 125–155. doi:10.4171/JNCG/51Google Scholar
[7] Emerson, H. and Meyer, R., Euler characteristics and Gysin sequences for group actions on boundaries. Math. Ann. 334(2006), no. 4, 853–904. doi:10.1007/s00208-005-0747-yGoogle Scholar
[8] Emerson, H. and Meyer, R., Equivariant Lefschetz maps for simplicial complexes and smooth manifolds. Math. Ann. 345(2009), no. 3, 599–630. doi:10.1007/s00208-009-0367-zGoogle Scholar
[9] Hartshorne, R., Algebraic geometry. Graduate Texts in Mathematics, 52, Springer-Verlag, New York, 1977.Google Scholar
[10] Kasparov, G. G., Equivariant KK-theory and the Novikov conjecture. Invent. Math. 91(1988), no. 1, 147–201. doi:10.1007/BF01404917Google Scholar
[11] Kaminker, J. and Putnam, I., K-theoretic duality of shifts of finite type. Comm. Math. Phys., 187(1997), no. 3, 509–522. doi:10.1007/s002200050147Google Scholar