Hostname: page-component-6dbcb7884d-vqfl6 Total loading time: 0 Render date: 2025-02-13T17:06:59.529Z Has data issue: false hasContentIssue false
  • English
  • Français

Lattice Paths with Diagonal Steps

Published online by Cambridge University Press:  20 November 2018

E. Goodman  and
T.V. Narayana
E. Goodman
Affiliation:
University of Alberta, Edmonton
T.V. Narayana
Affiliation:
University of Alberta, Edmonton
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

The André-Poincaré "probléme du scrutin" [9] can be stated as follows: In an election between two candidates A polls m votes, B polls n, m > n. If the votes are counted one by one what is the probability that A leads B throughout the counting? Many derivations and interpretations of the solution 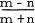have been given and a convenient summary of methods till 1956 can be found in Feller [1]. So numerous are the generalizations of ballot problems and their applications since this date that we do not even attempt an enumeration here.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 12 , Issue 6 , December 1969 , pp. 847 - 855
Copyright
Copyright © Canadian Mathematical Society 1969

References

1. Feller, W., An introduction to probability theory and its applications. (J. Wiley, New York, 1957).Google Scholar
2. Grossman, H.D., Fun with lattice points. Scripta Mathematica 15 (1949) 79–81.Google Scholar
3. Mohanty, S.G. and Handa, B.R., On lattice paths with several diagonal steps. Can. Math. Bull. 11 (1968) 537–545.Google Scholar
4. Moser, L. and Zayachkowski, W., Lattice paths with diagonal steps. Scripta Mathematica 26 (1961) 223–229.Google Scholar
5. Narayana, T. V., A problem in the theory of probability. J. Indian Soc. Agric. Statist. 6 (1954) 139–148.Google Scholar
6. Narayana, T.V., Sur les Treillis Formés par les Partitions d′un Entier et Leurs Applications à la Théorie des Probabilités. Comptes Rendus des Séances de l′Académie des Sciences, Paris, t. 240 (1955) 1188–1189.Google Scholar
7. Narayana, T.V., A partial order and its application to probability theory. Sankhyā: The Indian Journal of Statistics, 21 (1959) 91.Google Scholar
8. Narayana, T. V., An analogue of the multinomial theorem. Can. Math. Bull. 5 (1962) 43–50.Google Scholar
9. Poincaré, H., Calcul des Probabilités. (Gauthier Villars, Paris, 1913).Google Scholar
10. Rohatgi, V.K., A note on lattice paths with diagonal steps. Can. Math. Bull. 7 (1964) 470–472.Google Scholar
11. Stocks, D.R. Jr, Lattice paths in E3 with diagonal steps. Can. Math. Bull. 10 (1967) 653–658.Google Scholar