Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T22:00:16.358Z Has data issue: false hasContentIssue false
  • English
  • Français

A Lattice Isomorphism Theorem for Nonsingular Retractable Modules

Published online by Cambridge University Press:  20 November 2018

Zhou Zhengping
Zhou Zhengping*
Affiliation:
Department of Mathematics University of Iowa Iowa City, Iowa 52242 U.S.A.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

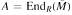Let RM be a nonsingular module such that B = EndR(M) is left nonsingular and has as its maximal left quotient ring, where 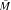is the injective hull of RM. Then it is shown that there is a lattice isomorphism between the lattice C(M) of all complement submodules of RM and the lattice C(B) of all complement left ideals of B, and that RM is a CS module if and only if B is a left CS ring. In particular, this is the case if RM is nonsingular and retractable.

Keywords

16D8016S90
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 37 , Issue 1 , 01 March 1994 , pp. 140 - 144
Copyright
Copyright © Canadian Mathematical Society 1994

References

1. Faith, C., Lectures on injective modules and quotient rings, Lecture Notes in Math. 49, Springer-Verlag, Heidelberg, 1967.Google Scholar
2. Goodearl, K. R. and Warfield, R. B., Jr., An introduction to noncommutative noetherian rings, Cambridge University Press, 1989.Google Scholar
3. Johnson, R. E. and Wong, E. T., Self-injective modules and quotient rings, Canad. Math. Bull. 2(1959), 167–173.Google Scholar
4. Khuri, S. M., Endomorphism rings of nonsingular modules, Ann. Sci. Math. Québec 4(1980), 145–152. 5 , Correspondence theorems for modules and their endomorphism rings, J. Algebra 122( 1989), 380- 396.Google Scholar
6. Khuri, S. M., Nonsingular retractable modules and their endomorphism rings, Bull. Austral. Math. Soc. 43 (1991), 63–71.Google Scholar
7. McConnell, J. C. and Robson, J. C., Noncommutative noetherian rings, John Wiley and Sons, 1987.Google Scholar
8. Stenström, B., Rings of quotients, Springer-Verlag, Berlin-Heidelberg-New York, 1975.Google Scholar