Hostname: page-component-586b7cd67f-gb8f7 Total loading time: 0 Render date: 2024-11-28T13:07:35.624Z Has data issue: false hasContentIssue false
  • English
  • Français

Krull Dimension of Injective Modules Over Commutative Noetherian Rings

Published online by Cambridge University Press:  20 November 2018

Patrick F. Smith
Patrick F. Smith*
Affiliation:
Department of Mathematics, University of Glasgow, Glasgow G12 8QW, Scotland, U.K.
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let $R$ be a commutative Noetherian integral domain with field of fractions 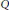$Q$. Generalizing a forty-year-old theorem of E. Matlis, we prove that the $R$-module 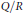$Q/R$ (or 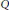$Q$) has Krull dimension if and only if $R$ is semilocal and one-dimensional. Moreover, if $X$ is an injective module over a commutative Noetherian ring such that $X$ has Krull dimension, then the Krull dimension of $X$ is at most 1.

Keywords

13E0516D5016P60
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 48 , Issue 2 , 01 June 2005 , pp. 275 - 282
Copyright
Copyright © Canadian Mathematical Society 2005

References

[1] Al-Huzali, A. H., Jain, S. K., and López-Permouth, S. R., Rings whose cyclics have finite Goldie dimension. J. Algebra 153(1992), 37–40.Google Scholar
[2] Camillo, V. P., Modules whose quotients have finite Goldie dimension. Pacific J. Math. 69(1977), 337–338.Google Scholar
[3] Dung, N. V., Huynh, D. V., Smith, P. F., and Wisbauer, R., Extending modules. Pitman Research Notes in Mathematics 313, Longman, Harlow, 1994.Google Scholar
[4] Faith, C., Quotient finite-dimensional modules with acc on subdirectly irreducible submodules are Noetherian. Comm. Algebra 27(1999), 1807–1810.Google Scholar
[5] Fisher, J. W., Finiteness conditions for projective and injective modules. Proc. Amer. Math. Soc. 40(1973), 389–394.Google Scholar
[6] Gordon, R. and Robson, J. C., Krull dimension. Memoirs of the American Mathematical Society 133, American Mathematical Society, Providence, RI, 1973.Google Scholar
[7] Izawa, T., Artinian endomorphism rings of projective modules. Rep. Fac. Sci. Shizuoka Univ. 16(1982), 17–23, and Correction ibid. 17 (1983), 1-2.Google Scholar
[8] Kaplansky, I., Commutative rings. Allyn and Bacon, Boston, 1970.Google Scholar
[9] Matlis, E., Some properties of Noetherian domains of dimension one. Canad. J. Math. 13(1961), 569–586.Google Scholar
[10] McConnell, J. C. and Robson, J. C., Noncommutative Noetherian rings. Wiley-Interscience, Chichester, 1987.Google Scholar
[11] Miller, R. and Turnidge, D., Some examples from infinite matrix rings. Proc. Amer.Math. Soc. 38(1973), 65–67.Google Scholar
[12] Passman, D. S., The algebraic structure of group rings. Wiley-Interscience,, New York, 1977.Google Scholar
[13] Sharpe, D.W. and Vámos, P., Injective modules. Cambridge Tracts in Mathematics and Mathematical Physics 62, Cambridge University Press, Cambridge, 1972.Google Scholar
[14] Vinsonhaler, C., Supplement to the paper “Orders in QF − 3rings”.. J. Algebra 17(1971), 149–151.Google Scholar
[15] Zariski, O. and Samuel, P., Commutative algebra. Vol 1 Van Nostrand, Princeton, NJ, 1958.Google Scholar