Hostname: page-component-586b7cd67f-l7hp2 Total loading time: 0 Render date: 2024-11-27T19:04:14.990Z Has data issue: false hasContentIssue false
  • English
  • Français

Kirszbraun’s Theorem via an Explicit Formula

Part of: Maps and general types of spaces defined by maps General convexity Nonlinear operators and their properties

Published online by Cambridge University Press:  29 April 2020

Daniel Azagra ,
Erwan Le Gruyer  and
Carlos Mudarra
Daniel Azagra*
Affiliation:
ICMAT (CSIC-UAM-UC3-UCM), Departamento de Análisis Matemático y Matemática Aplicada, Facultad Ciencias Matemáticas, Universidad Complutense, 28040, Madrid, Spain
Erwan Le Gruyer
Affiliation:
INSA de Rennes & IRMAR, 20, Avenue des Buttes de Coësmes, CS 70839 F-35708, Rennes Cedex 7, France e-mail: [email protected]
Carlos Mudarra
Affiliation:
ICMAT (CSIC-UAM-UC3-UCM), Calle Nicolás Cabrera 13-15. 28049Madrid, Spain e-mail: [email protected]
*
e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let 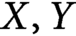$X,Y$ be two Hilbert spaces, let E be a subset of 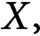$X,$ and let 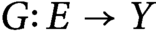$G\colon E \to Y$ be a Lipschitz mapping. A famous theorem of Kirszbraun’s states that there exists 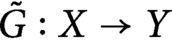$\tilde {G} : X \to Y$ with 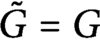$\tilde {G}=G$ on E and 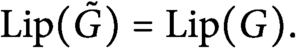$ \operatorname {\mathrm {Lip}}(\tilde {G})= \operatorname {\mathrm {Lip}}(G).$ In this note we show that in fact the function 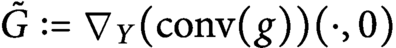$\tilde {G}:=\nabla _Y( \operatorname {\mathrm {conv}} (g))( \cdot , 0)$, where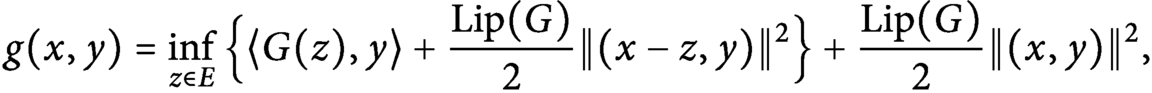

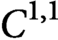$$\begin{align*}g(x,y) = \inf_{z \in E} \Big\lbrace \langle G(z), y \rangle + \frac{\operatorname{\mathrm{Lip}}(G)}{2} \|(x-z,y)\|^2 \Big\rbrace + \frac{\operatorname{\mathrm{Lip}}(G)}{2}\|(x,y)\|^2, \end{align*}$$
defines such an extension. We apply this formula to get an extension result for strongly biLipschitz mappings. Related to the latter, we also consider extensions of $C^{1,1}$ strongly convex functions.

Keywords

Lipschitz functionKirszbraun theorem

MSC classification

Primary: 47H09: Contraction-type mappings, nonexpansive mappings, $A$-proper mappings, etc.
Secondary: 52A41: Convex functions and convex programs 54C20: Extension of maps
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 1 , March 2021 , pp. 142 - 153
Check for updates
Creative Commons
Creative Common License - CCCreative Common License - BY
This is an Open Access article, distributed under the terms of the Creative Commons Attribution licence (http://creativecommons.org/licenses/by/4.0/), which permits unrestricted re-use, distribution, and reproduction in any medium, provided the original work is properly cited.
Copyright
© Canadian Mathematical Society 2020

Footnotes

D. Azagra and C. Mudarra were partially supported by Grant MTM2015-65825-P and by the Severo Ochoa Program for Centres of Excellence in R & D (Grant SEV-2015-0554).

References

Akopyan, A. V. and Tarasov, A. S., A constructive proof of Kirszbraun’s theorem. Mat. Zametki 84(2008), no. 5, 781–784. https://doi.org/10.1134/S000143460811014XGoogle Scholar
Aschenbrenner, M. and Fischer, A., Definable versions of theorems by Kirszbraun and Helly. Proc. London Math. Soc (3) 102(2011), 468–502. https://doi.org/10.1112/plms/pdq029CrossRefGoogle Scholar
Azagra, D. and Mudarra, C., Whitney Extension Theorems for convex functions of the classes ${C}^1$ and ${C}^{1,\omega }$. Proc. London Math. Soc. 114(2017), no. 1, 133–158. https://doi.org/10.1112/plms.12006CrossRefGoogle Scholar
Azagra, D., Le Gruyer, E., and Mudarra, C., Explicit formulas for ${C}^{1,1}$ and ${C}_{\mathrm{conv}}^{1,\omega }$ extensions of 1-jets in Hilbert and superreflexive spaces. J. Funct. Anal. 274(2018), 3003–3032. https://doi.org/10.1016/j.jfa.2017.12.007CrossRefGoogle Scholar
Bauschke, H. H., Fenchel duality, Fitzpatrick functions and the extension of firmly nonexpansive mappings. Proc. Amer. Math. Soc. 135(2007), 135–139. https://doi.org/10.1090/S0002-9939-06-08770-3CrossRefGoogle Scholar
Bauschke, H. H. and Combettes, P.L., Convex analysis and monotone operator theory in Hilbert spaces. 2nd ed., CMS Books in Mathematics, Springer, Cham, 2017. https://doi.org/10.1007/978-3-319-48311-5CrossRefGoogle Scholar
Bauschke, H. H., Moffat, S. M., and Wang, X., Firmly nonexpansive mappings and maximally monotone operators: correspondence and duality. Set-Valued Anal. 20(2012), 131–153. https://doi.org/10.1007/s11228-011-0187-7CrossRefGoogle Scholar
Bauschke, H. H. and Wang, X., The kernel average for two convex functions and its applications to the extension and representation of monotone operators. Trans. Amer. Math. Soc. 361(2009), 5947–5965. https://doi.org/10.1090/S0002-9947-09-04698-4CrossRefGoogle Scholar
Bauschke, H. H. and Wang, X., Firmly nonexpansive and Kirszbraun-Valentine extensions: a constructive approach via monotone operator theory. In: Nonlinear analysis and optimization I., Contemp. Math., 513, Israel Math. Conf. Proc., American Mathematical Society, Providence, RI, 2010, pp. 55–64. https://doi.org/10.1090/conm/513/10075Google Scholar
Benoist, J. and Hiriart-Urruty, J.-B., What is the subdifferential of the closed convex hull of a function?. SIAM J. Math. Anal. 27(1996), 1661–1679. https://doi.org/10.1137/S003614109465936CrossRefGoogle Scholar
Benyamini, Y. and Lindenstrauss, J., Geometric nonlinear functional analysis. Amer. Math. Soc. Coll. Pubs. 48, American Mathematical Society, Providence, RI, 2000.Google Scholar
Brudnyi, Y. ad Shvartsman, P., Whitney’s extension problem for multivariate ${C}^{1,\omega }$-functions. Trans. Amer. Math. Soc. 353(2001), 2487–2512. https://doi.org/10.1090/S0002-9947-01-02756-8CrossRefGoogle Scholar
Borwein, J. M. and Vanderwerff, J. D., Convex functions: constructions, characterizations and counterexamples. Encyclopedia of Mathematics and its Applications, 109, Cambridge University Press, Cambridge, 2010. https://doi.org/10.1017/CB09781139087322CrossRefGoogle Scholar
Daniilidis, A., Haddou, M., Le Gruyer, E., and Ley, O., Explicit formulas for ${C}^{1,1}$ Glaeser-Whitney extensions of 1-fields in Hilbert spaces. Proc. Amer. Math. Soc. 146(2018), 4487–4495. https://doi.org/10.1090/proc/14012CrossRefGoogle Scholar
Federer, H., Geometric measure theory. Die Grundlehren der mathematischen Wissenschaften, Band, 153, Springer-Verlag, New York, 1969.Google Scholar
Fefferman, C., A sharp form of Whitney’s extension theorem. Ann. of Math. (2) 161(2005), no. 1, 509–577. https://doi.org/10.4007/annals.2005.161.509CrossRefGoogle Scholar
Fefferman, C., Whitney’s extension problem for ${C}^m$. Ann. of Math. (2) 164(2006), no. 1, 313–359. https://doi.org/10.4007/annals.2006.164.313CrossRefGoogle Scholar
Fefferman, C., Whitney’s extension problems and interpolation of data. Bull. Amer. Math. Soc. (N.S.) 46(2009), no. 2, 207–220. https://doi.org/10.1090/S0273-0979-08-01240-8CrossRefGoogle Scholar
Ghomi, M., Strictly convex submanifolds and hypersurfaces of positive curvature. J. Differential Geom. 57(2001), 239–271.CrossRefGoogle Scholar
Ghomi, M., The problem of optimal smoothing for convex functions. Proc. Amer. Math. Soc. 130(2002), no. 8, 2255–2259. https://doi.org/10.1090/S0002-9939-02-06743-6CrossRefGoogle Scholar
Grünbaum, F. and Zarantonello, E.H., On the extension of uniformly continuous mappings. Michigan Math. J. 15(1968), 65–74.CrossRefGoogle Scholar
Kirchheim, B., Kristensen, J., Differentiability of convex envelopes. C. R. Acad. Sci. Paris Sér. I Math. 333(2001), no. 8, 725–728. https://doi.org/10.1016/S0764-4442(01)02117-6CrossRefGoogle Scholar
Kirszbraun, M. D., Über die zusammenziehenden und Lipschitzschen Transformationen. Fund. Math. 22(1934), 77–108.CrossRefGoogle Scholar
Le Gruyer, E., Minimal Lipschitz extensions to differentiable functions defined on a Hilbert space. Geom. Funct. Anal 19(2009), 1101–1118. https://doi.org/10.1007/s00039-009-0027-1CrossRefGoogle Scholar
Le Gruyer, E., Phan, Thanh-Viet, Sup-Inf explicit formulas for minimal Lipschitz extensions for $1$-fields on ${\mathbb{R}}^n$. J. Math. Anal. Appl. 424(2015), 1161–1185. https://doi.org/10.1016.j.jmaa.2014CrossRefGoogle Scholar
Mickle, E. J., On the extension of a transformation. Bull. Amer. Math. Soc. 55(1949), 160–164. https://doi.org/10.1090/S0002-9904-1949-09189-9CrossRefGoogle Scholar
Reich, S. and Simons, S., Fenchel duality, Fitzpatrick functions and the Kirszbraun-Valentine extension theorem. Proc. Amer. Math. Soc. 133(2005), 2657–2660. https://doi.org/10.1090/S0002-9939-05-07983-9CrossRefGoogle Scholar
Rockafellar, T., Convex analysis. Princeton Mathematical Series, 28, Princeton University Press, Princeton, NJ, 1970.CrossRefGoogle Scholar
Rockafellar, T. and Wets, R.J.-B., Variational analysis. Springer, New York, 1998.CrossRefGoogle Scholar
Valentine, F. A., A Lipschitz condition preserving extension for a vector function. Amer. J. Math. 67(1945), 83–93. https://doi.org/10.2307/2371917CrossRefGoogle Scholar
Yan, M., Extension of convex function. J. Convex Anal. 21(2014) no. 4, 965–987.Google Scholar
Wells, J. C., Differentiable functions on Banach spaces with Lipschitz derivatives. J. Differential Geometry 8(1973), 135–152.CrossRefGoogle Scholar