Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T19:38:54.302Z Has data issue: false hasContentIssue false
  • English
  • Français

Kahane-Khinchin’s Inequality for Quasi-Norms

Published online by Cambridge University Press:  20 November 2018

A. E. Litvak
A. E. Litvak*
Affiliation:
Department of Mathematics, Tel Aviv University, Ramat Aviv, Tel Aviv, Israel 69978, email: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We extend the recent results of R. Latała and O. Guédon about equivalence of 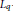${{L}_{q}}$ -norms of logconcave random variables (Kahane-Khinchin’s inequality) to the quasi-convex case. We construct examples of quasi-convex bodies 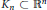${{K}_{n\,}}\subset {{\mathbb{R}}^{n}}$ which demonstrate that this equivalence fails for uniformly distributed vector on 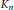${{K}_{n}}$ (recall that the uniformly distributed vector on a convex body is logconcave). Our examples also show the lack of the exponential decay of the “tail” volume (for convex bodies such decay was proved by M. Gromov and V. Milman).

Keywords

46B0952A3060B11
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 43 , Issue 3 , 01 September 2000 , pp. 368 - 379
Copyright
Copyright © Canadian Mathematical Society 2000

References

[BBP] Bastero, J., Bernués, J. and Peña, A., The theorem of Caratheodory and Gluskin for 0 < p < 1. Proc. Amer. Math. Soc. (1) 123 (1995), 141–144.Google Scholar
[Bor1] Borell, C., Convex measures on locally convex spaces. Ark.Mat. 12 (1974), 239–252.Google Scholar
[Bor2] Borell, C., Convex set functions in d-space. Period.Math.Hung. (2) 6 (1975), 111–136.Google Scholar
[Bou] Bourgain, J., On high dimensional maximal functions associated to convex bodies. American J. Math. 108 (1986), 1467–1476.Google Scholar
[DKH] Davidovic, J. S., Korenbljumand, B. I. Hacet, B. I., A property of logarithmically concave functions. Dokl. Acad. Nauk SSSR (6) 185 (1969), 477–480.Google Scholar
[GrM] Gromov, M. and Milman, V., Brunn theorem and a concentration of volume phenomena for symmetric convex bodies. Israel seminar on GAFA, V, Tel-Aviv, 1983–1984.Google Scholar
[Gu] Guédon, O., Kahane-Khinchine type inequalities for negative exponent. Preprint.Google Scholar
[KPR] Kalton, N. J., Peck, N. T. and Roberts, J. W., An F-space sampler. London Math. Soc. Lecture Note Ser. 89, Cambridge University Press, 1984.Google Scholar
[Kön] König, H., Eigenvalue Distribution of Compact Operators. Birkhäuser, 1986.Google Scholar
[La] Latała, R., On the equivalence between geometric and arithmetic means for logconcave measures. Convex Geometric Analysis (Berkeley, CA, 1996), 123–127;Math. Sci. Res. Inst. Publ. 34, Cambridge University Press, Cambridge, 1999.Google Scholar
[LMS] Litvak, A. E., Milman, V. D. and Schechtman, G., Averages of norms and quasi-norms. Math. Ann. (1) 312 (1998), 95–124.Google Scholar
[MP] Milman, V. D. and Pajor, A., Isotropic position and inertia ellipsoids and zonoids of the unit ball of a normed n-dimensional space. Geometric aspects of functional analysis, Israel Seminar 1987–88; Lecture Notes in Math. 1376(1989), Springer-Verlag, Berlin-New York, 64–104.Google Scholar
[MS] Milman, V. D. and Schechtman, G., Asymptotic theory of finite dimensional normed spaces. LectureNotes in Math. 1200, Springer-Verlag, 1986.Google Scholar
[Pr] Prékopa, A., Logarithmic concave measures with application to stochastic programming. Acta Sci. Math. (Szeged) 32 (1971), 301–316.Google Scholar
[R] Rolewicz, S.,Metric linear spaces.MonografieMatematyczne, Tom. 56. (MathematicalMonographs 56), PWN-Polish Scientific Publishers,Warsaw, 1972.Google Scholar
[U] Ullrich, D. C., An extension of the Kahane-Khinchine inequality in a Banach space. Israel J. Math. 62 (1988), 56–62.Google Scholar