Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T16:43:54.475Z Has data issue: false hasContentIssue false
  • English
  • Français

Involutions of RA Loops

Published online by Cambridge University Press:  20 November 2018

Edgar G. Goodaire  and
César Polcino Milies
Edgar G. Goodaire
Affiliation:
Memorial University of Newfoundland, St. John’s, Newfoundland A1C 5S7, Canada e-mail: [email protected]
César Polcino Milies
Affiliation:
Instituto de Matemática e Estatística, Universidade de São Paulo, Caixa Postal 66.281, CEP 05314-970, São Paulo SP, Brasil e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

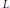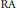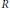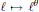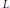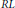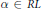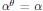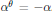Let $L$ be an $\text{RA}$ loop, that is, a loop whose loop ring over any coefficient ring $R$ is an alternative, but not associative, ring. Let $\ell \,\mapsto \,{{\ell }^{\theta }}$ denote an involution on $L$ and extend it linearly to the loop ring $RL$. An element $\alpha \,\in \,RL$ is symmetric if ${{\alpha }^{\theta }}\,=\,\alpha$ and skew-symmetric if ${{\alpha }^{\theta }}=-\alpha$ . In this paper, we show that there exists an involution making the symmetric elements of 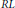$RL$ commute if and only if the characteristic of 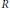$R$ is 2 or θ is the canonical involution on 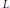$L$, and an involution making the skew-symmetric elements of 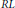$RL$ commute if and only if the characteristic of 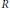$R$ is 2 or 4.

Keywords

20N0517D05
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 52 , Issue 2 , 01 June 2009 , pp. 245 - 256
Copyright
Copyright © Canadian Mathematical Society 2009

References

[CG86] Chein, O. and Goodaire, E. G., Loops whose loop rings are alternative. Comm. Algebra 14(1986), no. 2, 293–310.Google Scholar
[CM] Broche, O. Cristo and Milies, C. Polcino, Commutativity of skew symmetric elements in group rings. Proc. Edinb. Math. Soc. 50(2007), no. 1, 37–47.Google Scholar
[CM06] Cristo, O. Broche and Marín, M. Ruiz, Lie identities in symmetric elements in group rings: a survey. In: Groups, rings and group rings, Lecture Notes in Pure and AppliedMathematics 248, Chapman & Hall/CRC, Boca Raton, FL, 2006, pp. 43–55.Google Scholar
[Cri] Cristo, O. Broche, Commutativity of symmetric elements in group rings. J. Group Theory, 9(2006), no. 5, 673–683.Google Scholar
[GJM96] Goodaire, E. G., Jespers, E., and Milies, C. Polcino, Alternative loop rings. North-Holland Mathematics Studies 184, North-Holland, Amsterdam, 1996.Google Scholar
[GM96] Goodaire, E. G. and Milies, C. Polcino, Finite conjugacy in alternative loop algebras. Comm. Algebra 24(1996), no. 3, 881–889.Google Scholar
[GM03] Giambruno, A. and Milies, C. Polcino, Unitary units and skew elements in group algebras. Manuscripta Math. 111(2003), no. 2, 195–209.Google Scholar
[Goo83] Goodaire, E. G., Alternative loop rings. Publ. Math. Debrecen 30(1983), no. 1–2, 31–38.Google Scholar
[GP87] Goodaire, Edgar G. and Parmenter, M. M., Semisimplicity of alternative loop rings. Acta Math. Hungar. 50(1987), no. 3–4, 241–247.Google Scholar
[GSV98] Giambruno, A., Sehgal, S. K., and Valenti, A., Symmetric units and group identities. Manuscripta Math. 96(1998), no. 4, 443–461.Google Scholar
[JM05] Jespers, E. and Marín, M. Ruiz, Antisymmetric elements in group rings. J. Algebra Appl. 4(2005), no. 4, 341–353.Google Scholar
[JM06] Jespers, E. and Marín, M. Ruiz, On symmetric elements and symmetric units in group rings. Comm. Algebra 34(2006), no. 2, 727–736.Google Scholar
[Lee99] Lee, G. T., Group rings whose symmetric elements are Lie nilpotent. Proc. Amer. Math. Soc. 127(1999), no. 11, 3153–3159.Google Scholar
[Lee03] Lee, G. T., Nilpotent symmetric units in group rings. Comm. Algebra 31(2003), no. 2, 581–608.Google Scholar
[Sag61] Sagle, A. A., Malcev algebras. Trans. Amer.Math. Soc. 101(1961), 426–458.Google Scholar