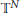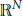Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
SETO, Michio
2005.
Submodules of $L^2(\mathbf{R}^2)$.
Tokyo Journal of Mathematics,
Vol. 28,
Issue. 2,
Bergqvist, Linus
2023.
Alternative proofs of Mandrekar’s theorem.
Proceedings of the American Mathematical Society, Series B,
Vol. 10,
Issue. 4,
p.
46.