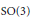Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Huizenga, Jack
and
Tapp, Kristopher
2007.
Invariant metrics with nonnegative curvature on SO(4) and other Lie groups.
Michigan Mathematical Journal,
Vol. 55,
Issue. 3,
Moghaddam, H R Salimi
2008.
The flag curvature of invariant (α, β)-metrics of type \frac{(\alpha+\beta)^2}{\alpha}.
Journal of Physics A: Mathematical and Theoretical,
Vol. 41,
Issue. 27,
p.
275206.
Moghaddam, Hamid Reza Salimi
2008.
On the Flag Curvature of Invariant Randers Metrics.
Mathematical Physics, Analysis and Geometry,
Vol. 11,
Issue. 1,
p.
1.
Schwachhöfer, Lorenz
and
Tapp, Kristopher
2009.
Homogeneous Metrics with Nonnegative Curvature.
Journal of Geometric Analysis,
Vol. 19,
Issue. 4,
p.
929.
Kerr, Megan M.
and
Kollross, Andreas
2013.
Nonnegatively curved homogeneous metrics in low dimensions.
Annals of Global Analysis and Geometry,
Vol. 43,
Issue. 3,
p.
273.
Mainkar, Meera
and
Schmidt, Benjamin
2019.
Metric foliations of homogeneous three-spheres.
Geometriae Dedicata,
Vol. 203,
Issue. 1,
p.
73.
Khan, Gabriel
and
Zhang, Jun
2020.
The Kähler geometry of certain optimal
transport problems.
Pure and Applied Analysis,
Vol. 2,
Issue. 2,
p.
397.
Sutton, Craig
2020.
On the Poisson relation for compact Lie groups.
Annals of Global Analysis and Geometry,
Vol. 57,
Issue. 4,
p.
537.
Lin, Samuel
Schmidt, Benjamin
and
Sutton, Craig
2021.
Geometric structures and the Laplace spectrum, Part II.
Transactions of the American Mathematical Society,
Vol. 374,
Issue. 12,
p.
8483.