No CrossRef data available.
Article contents
Invariant means on weakly almost periodic functionals with application to quantum groups
Published online by Cambridge University Press: 16 January 2023
Abstract
Let 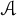 ${\mathcal A}$ be a Banach algebra, and let
${\mathcal A}$ be a Banach algebra, and let 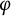 $\varphi $ be a nonzero character on
$\varphi $ be a nonzero character on 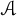 ${\mathcal A}$. For a closed ideal I of
${\mathcal A}$. For a closed ideal I of 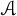 ${\mathcal A}$ with
${\mathcal A}$ with 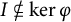 $I\not \subseteq \ker \varphi $ such that I has a bounded approximate identity, we show that
$I\not \subseteq \ker \varphi $ such that I has a bounded approximate identity, we show that 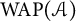 $\operatorname {WAP}(\mathcal {A})$, the space of weakly almost periodic functionals on
$\operatorname {WAP}(\mathcal {A})$, the space of weakly almost periodic functionals on 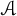 ${\mathcal A}$, admits a right (left) invariant
${\mathcal A}$, admits a right (left) invariant 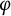 $\varphi $-mean if and only if
$\varphi $-mean if and only if 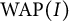 $\operatorname {WAP}(I)$ admits a right (left) invariant
$\operatorname {WAP}(I)$ admits a right (left) invariant 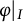 $\varphi |_I$-mean. This generalizes a result due to Neufang for the group algebra
$\varphi |_I$-mean. This generalizes a result due to Neufang for the group algebra 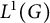 $L^1(G)$ as an ideal in the measure algebra
$L^1(G)$ as an ideal in the measure algebra 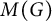 $M(G)$, for a locally compact group G. Then we apply this result to the quantum group algebra
$M(G)$, for a locally compact group G. Then we apply this result to the quantum group algebra 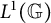 $L^1({\mathbb G})$ of a locally compact quantum group
$L^1({\mathbb G})$ of a locally compact quantum group 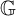 ${\mathbb G}$. Finally, we study the existence of left and right invariant
${\mathbb G}$. Finally, we study the existence of left and right invariant 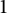 $1$-means on
$1$-means on 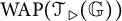 $ \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$.
$ \operatorname {WAP}(\mathcal {T}_{\triangleright }({\mathbb G}))$.
- Type
- Article
- Information
- Copyright
- © The Author(s), 2023. Published by Cambridge University Press on behalf of The Canadian Mathematical Society



