Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-28T18:00:58.141Z Has data issue: false hasContentIssue false
  • English
  • Français

Interpolation by Linear Sums of Harmonic Measures

Published online by Cambridge University Press:  20 November 2018

Marvin Ortel
Marvin Ortel*
Affiliation:
Stanford University, Stanford, California94305
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let α be an open arc on the unit circle

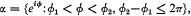
and for z=reiθ, 0 ≤ r < 1, let

(1)

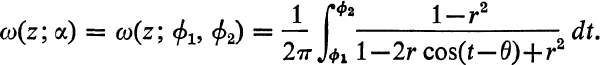
The function ω(z; α) is called the harmonic measure of the arc α with respect to the unit disc, (Nevanlinna 2); it is harmonic and bounded in the unit disc and possesses (Fatou) boundary values 1 and 0 at interior points of α and the complementary arc β respectively.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 18 , Issue 2 , June 1975 , pp. 249 - 253
Copyright
Copyright © Canadian Mathematical Society 1975

References

1. Ahlfors, L. and Sario, L., Riemann Surfaces, II, 3E, Princeton University Press, Princeton, 1960.Google Scholar
2. Nevanlinna, R., Analytic Functions, Springer, Berlin, 1970.Google Scholar
3. Walsh, J. L., The critical points of linear combinations of harmonic functions, Bull. Amer. Math. Soc, vol. 54 (1948), 191-195.Google Scholar
4. Walsh, J. L., The location of critical points of analytic and harmonic functions, American Mathematical Society, New York, 1950.Google Scholar