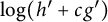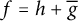Integral mean estimates for univalent and locally univalent harmonic mappings

Abstract

We verify a long-standing conjecture on the membership of univalent harmonic mappings in the Hardy space, whenever the functions have a “nice” analytic part. We also produce a coefficient estimate for these functions, which is in a sense best possible. The problem is then explored in a new direction, without the additional hypothesis. Interestingly, our ideas extend to certain classes of locally univalent harmonic mappings. Finally, we prove a Baernstein-type extremal result for the function $\log (h'+cg')$, when $f=h+\overline {g}$ is a close-to-convex harmonic function, and c is a constant. This leads to a sharp coefficient inequality for these functions.

1 Introduction

A central problem pertaining to the growth of univalent harmonic mappings is to determine the exact range of $p>0$ so that these functions belong to the harmonic Hardy space $h^p$ . The early developments in this direction were due to Abu-Muhanna and Lyzzaik [1], which were later improved by Nowak [17]. She proved sharp results for the classes of convex and close-to-convex harmonic functions, and conjectured an analogous range of p for the whole class $S_H$ of normalized univalent harmonic functions. The aim of this paper is to verify this conjecture for functions $f \in S_H$ with an additional property. The main theorems and their implications are presented in Section 2, while the proofs are given in Section 4. Section 3 contains results from the literature that are useful for our purpose.

A function f analytic in the open unit disk ${\mathbb D} = \{z: \; \vert z \vert <1\}$ is of class $H^p$ $(0 < p \le \infty )$ if the integral means

$$ \begin{align*}M_p(r, f) = \left\{ \begin{array}{ll} \displaystyle \left( \frac{1}{2\pi}\int_{0}^{2\pi}\vert f(r e^{i\theta}) \vert ^p d\theta \right)^{\frac{1}{p}}, \quad & 0 < p < \infty, \\ \displaystyle \sup_{ \vert z \vert=r} \vert f(z) \vert, \quad & p = \infty \end{array} \right.\end{align*} $$

remain bounded as $r \to 1^-$ . The norm of a function $f \in H^p$ is defined as ${\|f\|_p = \lim _{r \to 1^-} M_p(r,f).}$ Integral means and $H^p$ spaces play a fundamental role in studies concerning the growth of functions; we refer to the books [9, 14, 18] for a detailed survey.

A harmonic function f in the unit disk has a unique representation $f=h+\overline {g}$ , where h, g are analytic functions in $\mathbb {D}$ with $g(0)=0$ . The function f is locally univalent and sense-preserving if, and only if, the Jacobian $J_f(z)=\vert h'(z)\vert ^2-\vert g'(z)\vert ^2$ is positive for all $z \in {\mathbb D}$ . Let $S_H$ be the class of all sense-preserving univalent harmonic functions f in ${\mathbb D}$ , normalized by the conditions $h(0)=g(0)=h'(0)-1=0$ . Denote by $K_H$ and $C_H$ the subclasses of $S_H$ consisting of harmonic mappings onto convex and close-to-convex regions, respectively. Let $S_H^0=\{f=h+\overline {g} \in S_H : g'(0)=0\}$ , $K_H^0=K_H \cap S_H^0$ , and $C_H^0=C_H \cap S_H^0$ . Two leading examples of univalent harmonic functions are the harmonic Koebe function

$$ \begin{align*}K(z) = H(z) + \overline{G(z)} = \left(\frac{z-\frac{1}{2}z^2+\frac{1}{6}z^3}{(1-z)^3}\right) + \overline{\left(\frac{\frac{1}{2}z^2+\frac{1}{6}z^3}{(1-z)^3}\right)}\end{align*} $$

which maps ${\mathbb D}$ onto ${\mathbb C} \backslash (-\infty , -1/6]$ , and the function

$$ \begin{align*}L(z) = H_1(z) + \overline{G_1(z)} = \left(\frac{z-\frac{1}{2}z^2}{(1-z)^2}\right) + \overline{\left(\frac{-\frac{1}{2}z^2}{(1-z)^2}\right)}\end{align*} $$

which maps ${\mathbb D}$ onto the half-plane ${\operatorname {Re}\,}\{w\}>-1/2$ . It is obvious that $K \in C_H^0$ and ${L \in K_H^0}$ . More details on univalent harmonic functions can be found in [6, 10].

A harmonic function f is said to be of class $h^p$ $(0<p\le \infty )$ if $\|f\|_p < \infty $ . Let us give an account of the problem considered in this paper. Every function $f=h+\overline {g} \in S_H$ admits the representation

(1.1) $$ \begin{align} h(z) = z+\sum_{n=2}^{\infty} a_n z^n \quad \text{and} \quad g(z)=\sum_{n=1}^{\infty} b_n z^n.\end{align} $$

Let us define $\alpha =\sup _{f \in S_H} \vert a_2\vert $ . Then $\alpha $ has crucial influence in the growth of functions in $S_H$ (see [21] for an exposition). Interest in the boundary behavior of functions $f \in S_H$ was initiated by Abu-Muhanna and Lyzzaik [1], who proved that $f \in h^p$ for $p<1/(2\alpha +2)^2$ . Bshouty and Hengartner [5] proposed to find the exact range of $p>0$ for which $f \in h^p$ . In [17], Nowak improved the range to $p<1/\alpha ^2$ , and obtained the sharp results that $f \in h^p$ for $p<1/2$ (resp. $p<1/3$ ) whenever f is a convex (resp. close-to-convex) harmonic function. These observations led her to conjecture that if $f \in S_H$ , then $f \in h^p$ for $p<1/\alpha $ . The conjecture seems challenging, and in the relatively recent development [20], the authors verified it by confining interest to harmonic quasiconformal mappings.

In this paper, we first give a relation between $M_p(r,f)$ and $M_p(r,h')$ , which naturally allows us to check the boundedness of $\|f\|_p$ whenever $h'$ behaves “nicely.” As it turns out, this can be achieved by placing the simple restriction that $h'$ takes no value infinitely often. An analytic function $\varphi $ in ${\mathbb D}$ has valency m if $\varphi $ takes no value more than m times. More generally, let for a function $\varphi $ analytic in $\mathbb {D}$ , $W(R)$ denote the area (regions covered multiply being counted multiply) of the image of $\mathbb {D}$ under $\varphi $ that lies in the disk $|w|\le R$ . If $W(R)\le m\pi R^2$ for all $R>0$ , where m is a positive number, then we say that $\varphi $ has mean valency m. This notion is due to Spencer, who proved the following inequality on the integral means of such functions.

Theorem A [22]

If f has mean valency $m\ge 1$ , $f(0)=0$ , and $p>0$ , then

$$ \begin{align*}M_p^p(r,f) \le K \int_{0}^r \frac{M_\infty^p(s,f)}{s} ds,\end{align*} $$

where $K=K(m,p)$ is independent of f.

This result was initially proved by Prawitz (see [19, Theorem 5.1]) for univalent functions.

Over the years, extremal problems on the growth of univalent functions have been widely studied. Let $\mathcal {S}$ denote the class of univalent analytic functions f in ${\mathbb D}$ with $f(0)=f'(0)-1=0$ . A seminal result in this direction is the following inequality of Baernstein.

Theorem B [2]

If $f \in \mathcal {S}$ and $0<p<\infty $ , then

$$ \begin{align*}M_p(r,f) \le M_p(r,k),\end{align*} $$

where $k(z)=z/(1-z)^2$ is the Koebe function.

Baernstein’s theorem was extended to derivatives by Leung [15] and Brown [4] for certain subclasses of $\mathcal {S}$ . We refer to [3, 12, 13, 16] for more problems of this type. In [12], Girela obtained similar results for the functions $\log (f(z)/z)$ . These functions appear in the definition of logarithmic coefficients $\gamma _n$ of a function $f \in \mathcal {S}$ :

$$ \begin{align*}\log \frac{f(z)}{z} = 2 \sum_{n=1}^\infty \gamma_n z^n.\end{align*} $$

The logarithmic coefficients were instrumental in de Branges’ proof of the Bieberbach conjecture (see [8]). Girela’s work readily led to the sharp inequality

$$ \begin{align*}\sum_{n=1}^\infty \vert\gamma_n\vert^2 \le \frac{\pi^2}{6},\end{align*} $$

an important estimate earlier obtained by Duren and Leung [11]. Interestingly, Girela proved the following extremal result for close-to-convex functions.

Theorem C [12]

Let $f \in \mathcal {S}$ be close-to-convex, and let $0<p\le 2$ . Then

$$ \begin{align*}M_p(r, \log f') \le M_p(r, \log k'),\end{align*} $$

where k is the Koebe function.

On the other hand, similar problems for harmonic functions remained unexplored until very recently, when the present authors initiated the study of Baernstein-type inequalities for harmonic functions.

Theorem D [7]

Let $0<p<\infty $ . If $f=h+\overline {g} \in C_H^0$ , then

$$ \begin{align*}M_p(r,h') \le M_p(r,H') \quad \text{and} \quad M_p(r,g') \le M_p(r,G').\end{align*} $$

For $f=h+\overline {g} \in K_H^0$ , we have

$$ \begin{align*}M_p(r,h') \le M_p(r,H_1') \quad \text{and} \quad M_p(r,g') \le M_p(r,G_1').\end{align*} $$

The functions $H, G$ and $H_1, G_1$ come from the harmonic functions K and L, respectively.

To explore the logarithmic coefficients in the setting of a harmonic mapping ${f=h+\overline {g}}$ , it is not feasible to consider $f(z)/z$ , as this function need not be harmonic, neither is the logarithm of a harmonic function defined in the literature. One cannot consider the functions $(h(z)+cg(z))/z$ (c constant) either, since $h(z)+cg(z)$ may have zeros at points other than the origin. Therefore, proceeding along the line of Theorem C, the functions $\log (h'+cg')$ seem to be the most natural choice.

Thus, we conclude the paper with a harmonic analogue of Girela’s result: we prove that Theorem C remains true for the functions $\log (h'+cg')$ , whenever $f=h+\overline {g}$ is a close-to-convex harmonic function and c is a constant. This takes forward the authors’ earlier line of work in [7].

2 Main theorems and auxiliary results

As discussed, we start with the following simple but useful lemma, the proof of which is just a slight modification of standard techniques.

Lemma 1 Let $0 < p \le 1$ . Suppose $f=h+\overline {g}$ is a locally univalent, sense-preserving harmonic function in ${\mathbb D}$ with $f(0)=0$ . Then

$$ \begin{align*}M_p^p(r,f) \le C \int_{0}^{r} (r-s)^{p-1} M_p^p(s,h') ds, \end{align*} $$

where C is a constant independent of f.

This, together with Theorem D, immediately give integral mean estimates for convex and close-to-convex harmonic functions.

Corollary 1 Let $0 < p \le 1$ , then we have the inequalities

$$ \begin{align*} M_p(r,f) & \le C \int_{0}^{r} (r-s)^{p-1} M_p^p(s,H') ds, \, \mbox{ whenever } f \in C_H^0,\\ M_p(r,f) & \le C \int_{0}^{r} (r-s)^{p-1} M_p^p(s,H_1') ds, \, \mbox{ whenever } f \in K_H^0. \end{align*} $$

Remark 1 The estimates for $p> 1$ for these classes are already obtained in [7]. It is pertinent to mention that an elementary upper bound can be easily given in the case of convex harmonic functions. If $f=h+\overline {g}$ is convex, it is well known [6, Theorem 5.7] that h is close-to-convex, and $|g(z)|\le |h(z)|$ , $z \in {\mathbb D}$ . Therefore, from [19, Theorem 5.1], we have

$$ \begin{align*}M_p^p(r,f) \le 2^p M_p^p(r,h) \le 2^p p \int_{0}^r \frac{M_\infty^p(s,h)}{s} ds \le 2^p p \int_{0}^r s^{p-1} (1-s)^{-2p} ds.\end{align*} $$

The last integral is the incomplete beta function $B(r;p,1-2p)$ .

As a consequence of Lemma 1, we verify Nowak’s conjecture for certain functions in $S_H$ . Indeed, the result is true for a more general class of functions. Let us recall that a family $\mathcal {L}$ of harmonic functions in ${\mathbb D}$ is said to be linear invariant (see [21]) if for every $f=h+\overline {g}\in \mathcal {L}$ , the functions

$$ \begin{align*} T_\varphi(f(z)) =\frac{f(\varphi(z))-f(\varphi(0))}{\varphi'(0)h'(\varphi(0))}, \quad \varphi \in \operatorname{Aut}({\mathbb D}), \end{align*} $$

belong to $\mathcal {L}$ , where $\operatorname {Aut}({\mathbb D})$ denotes the set of analytic automorphisms of ${\mathbb D}$ . Our result does not require univalence, and holds for any linear invariant class $\mathcal {H}$ of locally univalent and sense-preserving harmonic functions (with usual normalizations), for which $\alpha (\mathcal {H})=\sup _{f \in \mathcal {H}} \vert a_2\vert $ is finite. For the remainder of this paper, we preserve the notation $\mathcal {H}$ to mean any such class of locally univalent harmonic functions.

Theorem 1 Let $f=h+\overline {g} \in S_H$ be such that $h'$ has finite mean valency. Then $f \in h^p$ for $p<1/\alpha $ . If $f \in \mathcal {H}$ and $h'$ has finite mean valency, then $f \in h^p$ for $p<1/\alpha (\mathcal {H})$ .

Lemma 1 also leads us to the following coefficient bound for these functions.

Theorem 2 Suppose $f=h+\overline {g} \in S_H$ has series representation (1.1), and $h'$ has finite mean valency. Then $\vert a_n \vert $ and $\vert b_n \vert $ are $O(n^{\alpha -1})$ , $n=2,3,4,\ldots $ . For $f \in \mathcal {H}$ with $h'$ having finite mean valency, $\vert a_n \vert $ and $\vert b_n \vert $ are $O(n^{\alpha (\mathcal {H})-1})$ .

Remark 2 This coefficient estimate for $f \in S_H$ is in a sense best possible. The conjectured value of $\alpha $ is $3$ . Given this, Theorem 2 asserts that $\vert a_n \vert $ and $\vert b_n \vert $ are $O(n^2)$ , which is the same order as in the harmonic analogue of the Bieberbach conjecture [6].

The problem, even without the assumption of finite mean valency, can be explored in another direction to produce a very interesting result. Since $S_H$ is known to be linear invariant, for $f=h+\overline {g} \in S_H$ and any $\zeta \in {\mathbb D}$ , the function

$$ \begin{align*}T(z)=\frac{f\left(\frac{z+\zeta}{1+\overline{\zeta}z}\right)-f(\zeta)}{(1-|\zeta|^2)h'(\zeta)}=A(z)+\overline{B(z)} \quad (z \in {\mathbb D})\end{align*} $$

again lies in $S_H$ . Let us write

$$ \begin{align*}A(z)=z+a_2(\zeta)z^2+a_3(\zeta)z^3+\cdots.\end{align*} $$

A customary computation gives

$$ \begin{align*}a_2(\zeta)=\frac{1}{2}\left\{(1-|\zeta|^2)\frac{h"(\zeta)}{h'(\zeta)}-2\overline{\zeta}\right\}.\end{align*} $$

Since $|a_2(\zeta )| \le \alpha $ , we find that

$$ \begin{align*}\left|\frac{h"(\zeta)}{h'(\zeta)}\right| \le \frac{C}{1-|\zeta|} \quad (\zeta \in {\mathbb D}),\end{align*} $$

for some positive constant C. However, this is the extreme bound on $h"/h'$ that a function $f=h+\overline {g} \in S_H$ can possess. In general, it is reasonable to expect a large subclass of $S_H$ to have slightly restricted growth, or more precisely, to exhibit the bound

$$ \begin{align*}\left|\frac{h"(\zeta)}{h'(\zeta)}\right| \le \frac{C}{(1-|\zeta|)^\beta} \quad (0 \le \beta <1).\end{align*} $$

The expression $h"/h'$ is of special interest in the theory of univalent functions. For example, it appears in the definition of the Schwarzian derivative, as well as in characterization results for certain geometric subclasses (e.g., convex and close-to-convex). The growth condition on $h"/h'$ leads us to the following result on the membership of univalent and locally univalent harmonic functions in the Hardy space.

Theorem 3 Let $f=h+\overline {g} \in S_H$ be such that

(2.1) $$ \begin{align} \left|\frac{h"(z)}{h'(z)}\right| \le \frac{C}{(1-|z|)^\beta},\end{align} $$

for some $\beta $ with $0 \le \beta <1$ . Then $f \in h^p$ for $p<2(1-\beta )/\alpha $ . Analogously, if $f=h+\overline {g} \in \mathcal {H}$ satisfies the growth estimate (2.1), then $f \in h^p$ for $p<2(1-\beta )/\alpha (\mathcal {H})$ .

Finally, we prove Girela’s result (Theorem C) in the setting of harmonic functions.

Theorem 4 Suppose $0 < p \le 2$ and $f =h+\overline {g}\in C_H^0$ . Then, for any constant $c \in {\mathbb D}$ , we have

$$ \begin{align*}M_p(r, \log (h'+cg')) \le M_p(r, \log (H'+G')).\end{align*} $$

The bound is sharp.

Like logarithmic coefficients in the case of analytic functions, it is interesting to study the power series coefficients of $\log (h'(z)+cg'(z))$ . Suppose $\log (h'(z)+cg'(z)) = \sum _{n=1}^\infty \lambda _n z^n$ . Then Theorem 4 has the following implication.

Corollary 2 For $f=h+\overline {g} \in C_H^0$ , we have the sharp inequality

$$ \begin{align*}\sum_{n=1}^\infty \vert\lambda_n\vert^2 \le \frac{14 \pi^2}{3}.\end{align*} $$

3 Preliminaries

Definition 1 [2]

For a real-valued function $g(x)$ integrable over $[-\pi ,\pi ]$ , the Baernstein star-function is defined as

$$ \begin{align*}g^*(\theta) = \sup_{\vert E\vert=2\theta} \int_{E} g(x) dx \quad (0 \le \theta \le \pi),\end{align*} $$

where $\vert E\vert $ is the Lebesgue measure of the set $E \subseteq [-\pi , \pi ]$ .

The following properties of the star-function are due to Leung [15].

Lemma A For $g,h \in L^1[-\pi , \pi ]$ ,

$$ \begin{align*}[g(\theta)+h(\theta)]^* \le g^*(\theta) + h^*(\theta).\end{align*} $$

Equality holds if g, h are both symmetric in $[-\pi , \pi ]$ and nonincreasing in $[0, \pi ]$ .

Lemma B If g, h are subharmonic functions in ${\mathbb D}$ and g is subordinate to h, then for each r in $(0,1)$ ,

$$ \begin{align*}g^*(r{e^{i\theta}}) \le h^*(r{e^{i\theta}}), \quad 0 \le \theta \le \pi.\end{align*} $$

Lemma C If $p(z)=e^{i\beta }+p_1z+\cdots $ is analytic and of positive real part in ${\mathbb D}$ , then

$$ \begin{align*}\left(\log\vert p(r{e^{i\theta}})\vert\right)^* \le \left(\log\left\vert\frac{1+r{e^{i\theta}}}{1-r{e^{i\theta}}}\right\vert\right)^*, \quad 0 \le \theta \le \pi.\end{align*} $$

An important feature in the proof of Lemma C is that a rotation factor does not affect the star-function. This observation will be suitably deployed in our work.

Definition 2 [12]

A domain D in ${\mathbb C}$ is said to be Steiner symmetric if its intersection with each vertical line is either empty or a segment placed symmetrically with respect to the real axis.

The next result by Girela is crucial in the proof of Theorem 4.

Lemma D [12]

Let F and $\mathcal {F}$ be analytic in $\overline {{\mathbb D}}$ and satisfy:

1. (i) $F(0)=\mathcal {F}(0)=0$ ,

2. (ii) $({\operatorname {Re}\,} F)^* \le ({\operatorname {Re}\,} \mathcal {F})^*$ in ${\mathbb D}^+=\{z \in {\mathbb D} : \; \operatorname {Im} z>0\}$ ,

3. (iii) $\displaystyle \min _{z\in {\mathbb D}} {\operatorname {Re}\,} \mathcal {F}(z) \le \min _{z\in {\mathbb D}} {\operatorname {Re}\,} F(z) \le \max _{z\in {\mathbb D}} {\operatorname {Re}\,} F(z) \le \max _{z\in {\mathbb D}} {\operatorname {Re}\,} \mathcal {F}(z)$ ,

4. (iv) $\mathcal {F}$ is univalent and $\mathcal {F}({\mathbb D})$ is a Steiner symmetric domain.

Then, for $0<p\le 2$ ,

$$ \begin{align*}\int_{-\pi}^{\pi} \vert F({e^{i\theta}})\vert^p d\theta \le \int_{-\pi}^{\pi} \vert \mathcal{F}({e^{i\theta}})\vert^p d\theta.\end{align*} $$

4 Proofs

4.1 Proof of Lemma 1

In what follows, C will denote a positive constant that is not necessarily the same at each occurrence. Let $\vert \nabla f\vert =(\vert h'\vert ^2+\vert g'\vert ^2)^{1/2}$ . For $0 \le r_1<r_2<1$ , we have

$$ \begin{align*} \vert f(r_2 {e^{i\theta}})-f(r_1 {e^{i\theta}})\vert & =\left\vert\int_{r_1}^{r_2} \frac{d}{d t} f(t {e^{i\theta}}) dt\right\vert\\ & \le \int_{r_1}^{r_2}\left\vert{e^{i\theta}} h'(t{e^{i\theta}}) + \overline{{e^{i\theta}} g'(t{e^{i\theta}})}\right\vert dt\\ & \le \sqrt{2} \int_{r_1}^{r_2} \left(\vert h'(t {e^{i\theta}})\vert^2 + \vert g'(t{e^{i\theta}})\vert^2\right)^{1/2} dt \\ & = \sqrt{2} \int_{r_1}^{r_2} \vert\nabla f(t {e^{i\theta}})\vert dt\\ & \le \sqrt{2} \left(r_2-r_1\right) \sup _{r_1 \le t \le r_2}\vert\nabla f(t {e^{i\theta}})\vert. \end{align*} $$

Since f is sense-preserving, i.e., $|g'(z)| < |h'(z)|$ for every $z \in {\mathbb D}$ , we find that

$$ \begin{align*}\vert\nabla f(t {e^{i\theta}})\vert \le \vert h'(t {e^{i\theta}})\vert+\vert g'(t {e^{i\theta}})\vert < 2 \vert h'(t {e^{i\theta}})\vert.\end{align*} $$

Therefore,

$$ \begin{align*} M_p^p(r_2,f)-M_p^p(r_1,f) & \le \frac{1}{2\pi} \int_{0}^{2\pi} \vert f(r_2 {e^{i\theta}})-f(r_1 {e^{i\theta}})\vert^p d\theta\\ & \le 2^{3p / 2}\left(r_2-r_1\right)^p \frac{1}{2\pi} \int_{0}^{2\pi} \left(\sup _{r_1 \le t \le r_2}\vert h'(t {e^{i\theta}})\vert\right)^p d\theta. \end{align*} $$

An appeal to the Hardy–Littlewood maximal theorem gives

$$ \begin{align*}\frac{1}{2\pi} \int_{0}^{2\pi} \left(\sup _{r_1 \le t \le r_2}\vert h'(t {e^{i\theta}})\vert\right)^p d\theta \le C M_p^p(r_2,h'),\end{align*} $$

so that

(4.1) $$ \begin{align} M_p^p(r_2,f)-M_p^p(r_1,f) \le C \left(r_2-r_1\right)^p M_p^p(r_2,h'). \end{align} $$

Let $0<r<1$ be arbitrary, and let $r_n=r(1-2^{-n})$ , $n=0,1,2,\ldots $ . Clearly, $M_p(0,f)=0$ as $f(0)=0$ . Using (4.1), we find that

$$ \begin{align*} M_p^p(r_{n+1},f) & =\sum_{k=1}^{n+1}\left[M_p^p(r_k,f)-M_p^p(r_{k-1},f)\right] \\ & \le C \sum_{k=1}^{n+1} (r_{k}-r_{k-1})^p M_p^p(r_k,h')\\ & = C \sum_{k=1}^{n+1} (r_{k}-r_{k-1}) (r-r_k)^{p-1} M_p^p(r_k,h'), \end{align*} $$

since $r_k-r_{k-1}=2^{-k}r=r-r_k$ . We now let $n \to \infty $ and obtain

$$ \begin{align*}M_p^p(r,f) \le C \int_{0}^{r} (r-s)^{p-1} M_p^p(s,h') ds\end{align*} $$

by means of Riemann integration.

4.2 Proof of Theorem 1

Let $1/(\alpha +1)<p \le 1$ and $f \in S_H$ . We may choose $r_n=1-2^{-n}$ in the proof of Lemma 1 to obtain

(4.2) $$ \begin{align} \| f\|_p^p \le C \int_{0}^{1} (1-s)^{p-1} M_p^p(s,h') ds, \end{align} $$

whenever the integral is finite. We break the integral in two parts, to separately deal with possible complications around $0$ and $1$ . For example, let us write

(4.3) $$ \begin{align} \| f\|_p^p \le C \left[\int_{0}^{1/4} (1-s)^{p-1} M_p^p(s,h') ds + \int_{1/4}^{1} (1-s)^{p-1} M_p^p(s,h') ds\right]. \end{align} $$

Throughout our computations, the constants will be denoted by C, K, etc., and they need not be the same at each occurrence. We do this for convenience, as constants do not affect our purpose.

We appeal to Theorem A for an estimate of $M_p^p(s,h')$ . Since $h'$ is finitely mean valent, so is $zh'$ . Therefore, we have

(4.4) $$ \begin{align} M_p^p(s,zh') \le K \int_{0}^s \frac{M_\infty^p(r,zh')}{r} dr. \end{align} $$

It is known (see [10, p. 98]) that

(4.5) $$ \begin{align} M_\infty(r,h') \le \frac{(1+r)^{\alpha-1}}{(1-r)^{\alpha+1}}.\end{align} $$

This, together with (4.4), implies

(4.6) $$ \begin{align} M_p^p(s,h') \le \frac{K}{s^p} \int_{0}^s \frac{r^{p-1}}{(1-r)^{(\alpha+1)p}} dr.\end{align} $$

For $s \le 1/4$ ,

$$ \begin{align*}M_p^p(s,h') \le \frac{K}{s^p} \int_{0}^{1/4} \frac{r^{p-1}}{(1-r)^{(\alpha+1)p}} dr \le \frac{K_1}{s^p} \int_{0}^{1/4} r^{p-1} dr \le \frac{K_2}{s^p} \quad (\text{as } p \le 1).\end{align*} $$

For $s> 1/4$ ,

$$ \begin{align*} M_p^p(s,h') & \le \frac{K}{s^p} \int_{0}^{1/4} \frac{r^{p-1}}{(1-r)^{(\alpha+1)p}} dr + \frac{K}{s^p} \int_{1/4}^{s} \frac{r^{p-1}}{(1-r)^{(\alpha+1)p}} dr\\ & \le \frac{K_2}{s^p} + K_3 \int_{1/4}^{s} \frac{dr}{(1-r)^{(\alpha+1)p}} \\& = \frac{K_2}{s^p} + \frac{K_3}{(\alpha+1)p-1} \left[\frac{1}{(1-s)^{(\alpha+1)p-1}} - K_4\right] \quad (\text{as } p>1/(\alpha+1))\\ & \le \frac{K_2}{s^p} + \frac{K_5}{(1-s)^{(\alpha+1)p-1}}. \end{align*} $$

Substituting these bounds in (4.3), we see that

$$ \begin{align*} \| f\|_p^p & \le C_1 \int_{0}^{1/4} s^{-p} (1-s)^{p-1} ds + C_1 \int_{1/4}^{1} s^{-p} (1-s)^{p-1} ds + C_2 \int_{1/4}^{1} \frac{ds}{(1-s)^{p\alpha}}\\ & = C_1 \int_{0}^{1} s^{-p} (1-s)^{p-1} ds + C_2 \int_{1/4}^{1} \frac{ds}{(1-s)^{p\alpha}}. \end{align*} $$

The first integral is the beta function $B(1-p,p)$ and converges for every $p\in (0,1)$ . The second integral is finite for $p<1/\alpha $ . Therefore, $f \in h^p$ for $p < 1/\alpha $ .

To prove the result for $f \in \mathcal {H}$ , we just need to establish the bound

$$ \begin{align*}M_\infty(r,h') \le \frac{(1+r)^{\alpha(\mathcal{H})-1}}{(1-r)^{\alpha(\mathcal{H})+1}}.\end{align*} $$

The argument presented here is well known (see, for example, [10, p. 98]), and will be useful in the later results. Since $\mathcal {H}$ is linear invariant, for any $\zeta \in {\mathbb D}$ , the function

$$ \begin{align*}T(z)=\frac{f\left(\frac{z+\zeta}{1+\overline{\zeta}z}\right)-f(\zeta)}{(1-|\zeta|^2)h'(\zeta)}=A(z)+\overline{B(z)} \quad (z \in {\mathbb D})\end{align*} $$

is in $\mathcal {H}$ . We write

$$ \begin{align*}A(z)=z+a_2(\zeta)z^2+a_3(\zeta)z^3+\cdots,\end{align*} $$

so that

$$ \begin{align*}a_2(\zeta)=\frac{1}{2}\left\{(1-|\zeta|^2)\frac{h"(\zeta)}{h'(\zeta)}-2\overline{\zeta}\right\}.\end{align*} $$

Since $|a_2(\zeta )| \le \alpha (\mathcal {H})$ , we find that

$$ \begin{align*}\frac{2r^2-2r\alpha(\mathcal{H})}{1-r^2} \le {\operatorname{Re}\,}\left\{\frac{zh"(z)}{h'(z)}\right\} \le \frac{2r^2+2r\alpha(\mathcal{H})}{1-r^2} \quad (|z|=r),\end{align*} $$

which is equivalent to

$$ \begin{align*}\frac{2r-2\alpha(\mathcal{H})}{1-r^2} \le \frac{\partial}{\partial r} \{\log |h'(r{e^{i\theta}})|\} \le \frac{2r+2\alpha(\mathcal{H})}{1-r^2}.\end{align*} $$

Now we integrate from $0$ to r to reach the estimate

(4.7) $$ \begin{align} \frac{(1-r)^{\alpha(\mathcal{H})-1}}{(1+r)^{\alpha(\mathcal{H})+1}} \le |h'(z)| \le \frac{(1+r)^{\alpha(\mathcal{H})-1}}{(1-r)^{\alpha(\mathcal{H})+1}}.\end{align} $$

The rest of the proof follows through an identical argument, and the details are omitted.

4.3 Proof of Theorem 2

We see that

$$ \begin{align*}(n+1) \vert a_{n+1}\vert= \left\vert\frac{1}{2\pi i} \int_{\vert z\vert=r}\frac{h'(z)}{z^{n+1}} dz \right\vert \le r^{-n} M_1(r,h').\end{align*} $$

We see from (4.6), for $p=1$ , that

$$ \begin{align*}M_1(r,h') \le \frac{K}{r} \int_{0}^r \frac{ds}{(1-s)^{\alpha+1}} \le \frac{K}{r(1-r)^{\alpha}},\end{align*} $$

for some absolute constant K which varies through occurrences. Therefore,

$$ \begin{align*}(n+1) \vert a_{n+1}\vert \le \frac{K}{r^{n+1}(1-r)^{\alpha}}.\end{align*} $$

The function on the right-hand side attains a minimum at $r=(n+1)/(n+1+\alpha )$ . With this choice of r, we obtain

$$ \begin{align*}(n+1) \vert a_{n+1}\vert \le K \left(1+\frac{\alpha}{n+1}\right)^{n+1} \left(n+1+\alpha\right)^{\alpha} \le K (n+1)^{\alpha}.\end{align*} $$

Therefore, replacing $n+1$ by n,

$$ \begin{align*}|a_n| \le K n^{\alpha-1}.\end{align*} $$

Using a similar argument, one can show that $\vert b_n \vert \le K n^{\alpha -1}$ . The proof for the second part of the theorem is identical, except for $\alpha $ suitably replaced by $\alpha (\mathcal {H})$ .

4.4 Proof of Theorem 3

The Hardy–Stein identity (see [19, p. 126]) for the function $h'$ implies that

$$ \begin{align*}\frac{d}{dr}\left[r\frac{d}{dr}M_p^p(r,h')\right]=\frac{p^2r}{2\pi} \int_{0}^{2\pi} |h'(r{e^{i\theta}})|^{p-2}|h"(r{e^{i\theta}})|^2 d\theta.\end{align*} $$

Since $M_p^p(r,h')$ is a (strictly) increasing function of r, we have

$$ \begin{align*}\frac{d}{dr}M_p^p(r,h')>0.\end{align*} $$

Therefore,

$$ \begin{align*} \frac{d^2}{dr^2}M_p^p(r,h') & \le \frac{p^2}{2\pi} \int_{0}^{2\pi} |h'(r{e^{i\theta}})|^{p-2}|h"(r{e^{i\theta}})|^2 d\theta\\ & = \frac{p^2}{2\pi} \int_{0}^{2\pi} |h'(r{e^{i\theta}})|^{p}\left|\frac{h"(r{e^{i\theta}})}{h'(r{e^{i\theta}})}\right|{}^2 d\theta\\ & \le \frac{p^2}{2\pi} \int_{0}^{2\pi} \frac{(1+r)^{(\alpha-1)p}}{(1-r)^{(\alpha+1)p}} \cdot \frac{C^2}{(1-r)^{2\beta}} \, d\theta \quad \left(\text{by } (4.5)\right)\\ & \le \frac{K}{(1-r)^{(\alpha+1)p+2\beta}}, \end{align*} $$

for some positive constant K, which is not the same in subsequent occurrences. Integrating twice from $0$ to s $(s<1)$ , we arrive at the estimate

$$ \begin{align*}M_p^p(s,h') \le \frac{K}{(1-s)^{(\alpha+1)p+2\beta-2}}.\end{align*} $$

Thus, an appeal to (4.2) gives

$$ \begin{align*}\| f\|_p^p \le C \int_{0}^{1} (1-s)^{p-1} M_p^p(s,h') ds \le C \int_{0}^{1} \frac{ds}{(1-s)^{\alpha p +2\beta-1}}.\end{align*} $$

The last integral converges for $\alpha p +2\beta -1<1$ , or equivalently, $p<2(1-\beta )/\alpha $ . Therefore, $f \in h^p$ for $p<2(1-\beta )/\alpha $ .

The proof for $f \in \mathcal {H}$ is similar, one only needs to replace $\alpha $ by $\alpha (\mathcal {H})$ , wherever applicable.

4.5 Proof of Theorem 4

Let $0<r<1$ and write

$$ \begin{align*}F(z) = \log(h'(rz)+cg'(rz)), \quad \mathcal{F}(z) = \log (H'(rz)+G'(rz)).\end{align*} $$

Clearly, $F(0)=\mathcal {F}(0)=0$ . Lemma 4 of [23] implies that there exist real numbers $\mu $ , $\theta _0$ and an analytic function $Q(z)$ with positive real part, such that

$$ \begin{align*}{\operatorname{Re}\,}\left\{Q(z)\left[ie^{i\theta_0} \left(1-z^2\right)\left(e^{-i\mu}h'(e^{i\theta_0}z)+e^{i\mu}g'(e^{i\theta_0}z)\right)\right]\right\}> 0, \quad z\in {\mathbb D}.\end{align*} $$

Let

$$ \begin{align*}P(z)=Q(z)\left[ie^{i\theta_0} \left(1-z^2\right)\left(e^{-i\mu}h'(e^{i\theta_0}z)+e^{i\mu}g'(e^{i\theta_0}z)\right)\right].\end{align*} $$

Without any loss of generality, we may assume $\vert Q(0)\vert =1$ , so that $\vert P(0)\vert =1$ . Since $Q(z)$ has positive real part, so does $1/Q(z)$ . The dilatation $w(z) = g'(z)/h'(z)$ satisfies $w(0)=0$ and $\vert w(z)\vert <1$ for all $z \in {\mathbb D}$ . We see that

$$ \begin{align*} \log\vert h'(e^{i\theta_0}z)+c g'(e^{i\theta_0}z)\vert & =\log \vert P(z)\vert +\log\left\vert\frac{1}{Q(z)}\right\vert +\log\left\vert\frac{1}{1-z^2}\right\vert\\ & \qquad +\log\left\vert\frac{1}{1+e^{2i\mu}w(e^{i\theta_0}z)}\right\vert+ \log\vert1+cw(e^{i\theta_0}z)\vert. \end{align*} $$

In view of Lemmas A–C, we have for $z \in {\mathbb D}^+$ ,

$$ \begin{align*} (\log\vert h'(z)+cg'(z)\vert)^* & \le \left(\log\left\vert\frac{1+z}{1-z}\right\vert\right)^* + \left(\log\left\vert\frac{1+z}{1-z}\right\vert\right)^*\\ & \quad +\left(\log\left\vert\frac{1}{1-z^2}\right\vert\right)^*+\left(\log\left\vert\frac{1}{1-z}\right\vert\right)^* +\left(\log\vert 1+z\vert\right)^*,\end{align*} $$

which implies

$$ \begin{align*}(\log\vert h'(z)+cg'(z)\vert)^* \le \left(\log\left\vert \frac{(1+z)^2}{(1-z)^4}\right\vert\right)^* = \left(\log\vert H'(z)+G'(z) \vert\right)^*,\end{align*} $$

i.e., $({\operatorname {Re}\,} F)^* \le ({\operatorname {Re}\,} \mathcal {F})^*$ . For $f=h+\overline {g} \in C_H^0$ , the function $f+c \overline {f} \in C_H$ for every constant $c \in {\mathbb D}$ . Also, it is known that $C_H$ is linear invariant and $\alpha (C_H)=3$ . Therefore, (4.7) leads to the inequalities

$$ \begin{align*}\frac{(1-r)^2}{(1+r)^4} \le |h'(r{e^{i\theta}})+cg'(r{e^{i\theta}})| \le \frac{(1+r)^2}{(1-r)^4},\end{align*} $$

so that

$$ \begin{align*}\min_{z\in {\mathbb D}} {\operatorname{Re}\,} \mathcal{F}(z) \le \min_{z\in {\mathbb D}} {\operatorname{Re}\,} F(z) \le \max_{z\in {\mathbb D}} {\operatorname{Re}\,} F(z) \le \max_{z\in {\mathbb D}} {\operatorname{Re}\,} \mathcal{F}(z).\end{align*} $$

That $\mathcal {F}$ is univalent and $\mathcal {F}({\mathbb D})$ is a Steiner symmetric domain can be proved using an argument similar to the one presented in [12, Lemma 1], we include the details below for the convenience of the reader. Therefore, the proof of the theorem is completed through an appeal to Lemma D. Since the harmonic Koebe function $K=H+\overline {G}\in C_H^0$ , the sharpness can be seen by letting $c \to 1^-$ .

Proposition 1 Let $\mathcal {G}(z) = \log (H'(z)+G'(z))$ . Then $\mathcal {G}$ is univalent and $\mathcal {G}({\mathbb D})$ is a Steiner symmetric domain.

Proof For $0<r<1$ , we see that

$$ \begin{align*}{\operatorname{Re}\,} \mathcal{G}(r e^{i \theta})=\log \frac{1}{\left|1-r e^{i \theta}\right|{}^2}+2 \log \left|\frac{1+r e^{i \theta}}{1-r e^{i \theta}}\right|. \end{align*} $$

Thus, $\operatorname {Re} \mathcal {G}(r e^{i \theta })$ is symmetric with respect to $\theta $ on $[-\pi , \pi ]$ , and strictly decreases on $[0, \pi ]$ . It is easy to see that $\operatorname {Im} \mathcal {G}(r e^{i \theta })>0$ in $0<\theta <\pi $ , because the same holds for $\log \left (1 /(1-z)^2\right )$ and $\log ((1+z) /(1-z))$ . Also, $\mathcal {G}(r e^{-i \theta })=\overline {\mathcal {G}(r e^{i \theta })}$ . Therefore, $\mathcal {G}$ is injective on $|z|=r$ and hence the argument principle implies that $\mathcal {G}$ is univalent in $|z| \le r$ . Finally, $\mathcal {G}$ maps $\{|z|=r\}$ onto a simple closed curve, which is symmetric with respect to the real axis, with decreasing real part for $\theta $ increasing from 0 to $\pi $ . This shows that $\mathcal {G}(|z|<r)$ is a Steiner symmetric domain. As this is true for every $r \in (0,1)$ , the desired conclusion follows.

Remark 3 The restriction $0<p\le 2$ in Theorem 4 is imposed by Lemma D. In other words, we do not know if Theorem 4 remains valid for $p>2$ .

4.6 Proof of Corollary 2

Let $\log (H'(z)+G'(z)) =\sum _{n=1}^\infty c_n z^n$ . Through a routine computation, we see that

$$ \begin{align*}c_n=\frac{2(2-(-1)^n)}{n}.\end{align*} $$

For $p=2$ , Theorem 4 gives

$$ \begin{align*}\sum_{n=1}^\infty \vert\lambda_n\vert^2 r^{2n} \le \sum_{n=1}^\infty \vert c_n\vert^2 r^{2n}.\end{align*} $$

Letting $r \to 1$ , we obtain

$$ \begin{align*}\sum_{n=1}^\infty \vert\lambda_n\vert^2 \le \sum_{n=1}^\infty \vert c_n\vert^2 = \frac{14\pi^2}{3}.\end{align*} $$

The sharpness follows from Theorem 4.