Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T01:58:53.102Z Has data issue: false hasContentIssue false
  • English
  • Français

Integral Functionals in the Duals of Lλ-Spacesc(1)

Published online by Cambridge University Press:  20 November 2018

H. W. Ellis  and
J. D. Hiscocks
H. W. Ellis
Affiliation:
Queen's University, Kingston, Ontario
J. D. Hiscocks
Affiliation:
University of Lethbridge, Lethbridge, Alberta
Rights & Permissions [Opens in a new window]

Extract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Luxemburg and Zaanen [5] call an element φ of the topological dual of a normed or seminormed vector space V an integral if

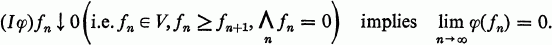
We denote the space of integrals by VI, For the Lλ function spaces introduced by Ellis and Halperin [2] another Banach subspace of the dual emerges, namely the conjugate space Lλ* which is the Lλ space determined by the conjugate length function λ*-Lλ* is contained in (Lλ)I but need not coincide with it.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 15 , Issue 4 , December 1972 , pp. 489 - 499
Copyright
Copyright © Canadian Mathematical Society 1972

Footnotes

(1)

Work supported in part by National Research Council Grant 3071.

References

1. Banach, S., Théorie des opérations linéaires, Monografje Matematyczne Warsaw, 1932.Google Scholar
2. Ellis, H. W. and Israel Halperin, Function spaces determined by a levelling length function, Canad. J. Math. 5 (1963), 576-592.Google Scholar
3. Ellis, H. W. and Snow, D. O., On (L1)* for general measure spaces, Canad. Math. Bull. 6(1963), 211-230.Google Scholar
4. Halperin, Israel, Reflexivity in the Lλ function spaces, Duke Math. J. 21 (1954), 205-208.Google Scholar
5. Luxemburg, W. A. J. and Zaanen, A. C., Notes on Banach function spaces, Proc. Acad. Science, Amsterdam, (Indag. Math). Note V, A. 66 (1963), 496-504; Note VI, A. 66 (1963), 655-668.Google Scholar