Article contents
Insolvability of 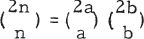
Published online by Cambridge University Press: 20 November 2018
Extract
A number of interesting Diophantine equations are of the a form f(n) = f(a) f(b). Thus the case f(a) = aa has been studied by C. Ko [2] and W. H. Mills [3] and a class of non-trivial solutions has been found, though whether these give all the solutions is still unsettled. The case f(n) = n! has been mentioned by W. Sierpinski. Here the situation is that besides the trivial solutions m! = m! 1! and (m!-1)! m! = (m!)! and the special solution 10! =7! 6! no other solutions are known, nor are they known not to exist. In the present note we show that the equation in the title has no solutions. A sketch of a somewhat different proof that this equation has at most a finite number of solutions was recently communicated to the author by P. Erdös.
- Type
- Notes on Number Theory V
- Information
- Copyright
- Copyright © Canadian Mathematical Society 1963
References
- 9
- Cited by


