Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-24T13:52:17.916Z Has data issue: false hasContentIssue false
  • English
  • Français

Injective and Weakly Injective Rings

Published online by Cambridge University Press:  20 November 2018

B. J. Gardner  and
P. N. Stewart
B. J. Gardner
Affiliation:
Mathematics Department, University of TasmaniaG.P.O. Box 252-C Hobart, Tasmania 7001, Australia
P. N. Stewart
Affiliation:
Department of Mathematics, Statistics and Computing Science, Dalhousie UniversityHalifax, Nova Scotia B3H 3J5, Canada
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let V be a variety of rings and let A ∊ V. The ring A is injective in V if every triangle

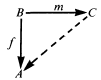
with C ∊ V, m a monomorphism and f a homomorphism has a commutative completion as indicated. A ring which is injective in some variety (equivalently, injective in the variety it generates) is called injective. When only triangles with f surjective are considered we obtain the notion of weak injectivity. Directly indecomposable injective and weakly injective rings are classified.

Keywords

16A5208B30
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 31 , Issue 4 , 01 December 1988 , pp. 487 - 494
Copyright
Copyright © Canadian Mathematical Society 1988

References

1. Davey, B. A. and L. G. Kovács, Absolute subretracts and weak injectives in congruence modular varieties Trans. A.M.S. 297(1986), pp. 181–196.Google Scholar
2. Procesi, C., Rings with Polynomial Identity (Marcel Dekker, New York, 1973).Google Scholar
3. Raphaël, R, Injective rings Comm. Algebra 1 (1974), pp. 403–414.Google Scholar
4. Rowen, L. H., Polynomial Identities in Ring Theory (Academic Press, New York, 1980).Google Scholar