Hostname: page-component-586b7cd67f-dlnhk Total loading time: 0 Render date: 2024-11-23T21:18:20.270Z Has data issue: false hasContentIssue false
  • English
  • Français

Infinite Geometric Products

Published online by Cambridge University Press:  20 November 2018

M. K. Vagholkar  and
P. J. Staff
M. K. Vagholkar
Affiliation:
School of Mathematics, University of New South Wales, Australia
P. J. Staff
Affiliation:
School of Mathematics, University of New South Wales, Australia
Rights & Permissions [Opens in a new window]

Summary

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

This paper is concerned with the infinite geometric products

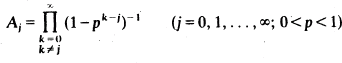
and their generalizations to higher dimensions. Some new expressions and identities are derived for these products by using stochastic theory. The function 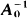is tabulated for p = 0(0.01)1.

Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 20 , Issue 3 , 01 September 1977 , pp. 359 - 367
Copyright
Copyright © Canadian Mathematical Society 1977

References

1. Abramowitz, M. and Stegun, I. A., Handbook of Mathematical Functions. Nat. Bur. Stand. Appl. Maths. Ser. 55 (1965).Google Scholar
2. Andrews, G. E., Subbarao, M. V. and Vidyasagar, H., A Family of Combinatorial Identities. Canad. Math. Bull. 15 (1972), 11-18.Google Scholar
3. Hardy, G. H., Collected Papers of G. H. Hardy. Clarendon Press, Oxford (1965).Google Scholar
4. Hardy, G. H. and Ramanujan, S., Une Formule Asymptotique Pour le Nombre des Partitions de n, Comptes Rendus 164 (1917), 35-38.Google Scholar
5. Hardy, G. H. and Ramanujan, S., Asymptotic Formulae in Combinatory Analysis. Proc. Lond. Math. Soc. (2), 17 (1918), 75-115.Google Scholar
6. Hardy, G. H. and Wright, E. M., An Introduction to the Theory of Numbers. Clarendon Press, Oxford (4th Ed.) 1968.Google Scholar
7. Katti, S. K., Interrelations Among Generalized Distributions and Their Components. Biometrics 22 (1966), 44-52.Google Scholar
8. Rademacher, H., On the Partition Function p(n). Proc. Lond. Math. Soc. (2), 43 (1937), 241-254.Google Scholar
9. Staff, P. J. and Vagholkar, M. K., Stationary Distributions of Open Markov Processes in Discrete Time with Application to Hospital Planning. J. Appl. Prob. 8 (1971), 668-680. Google Scholar