Inequalities for Eigenvalues of a General Clamped Plate Problem

Abstract

Let 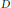$D$ be a connected bounded domain in 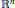${{\mathbb{R}}^{n}}$. Let 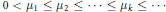$0\,<\,{{\mu }_{1}}\,\le \,{{\mu }_{2}}\,\le \,\cdots \,\le \,{{\mu }_{k}}\,\le \,\cdots $ be the eigenvalues of the following Dirichlet problem:

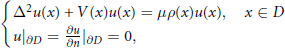$$\left\{ \begin{align} & {{\Delta }^{2}}u(x)\,+\,V(x)u(x)\,=\,\mu \rho (x)u(x),x\in \,D \\ & u{{|}_{\partial D}}\,=\,\frac{\partial u}{\partial n}\,{{|}_{\partial D}}\,=\,0, \\ \end{align} \right.$$

where 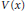$V(x)$ is a nonnegative potential, and 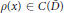$\rho (x)\,\in \,C(\overset{-}{\mathop{D}}\,)$ is positive. We prove the following inequalities:

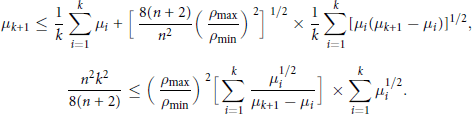$$\begin{align} & {{\mu }_{k+1}}\le \frac{1}{k}\sum\limits_{i=1}^{k}{\mu i+}{{[\frac{8(n+2)}{{{n}^{2}}}{{\left( \frac{\rho \max }{\rho \min } \right)}^{2}}]}^{1/2}}\times \frac{1}{k}{{\sum\limits_{i=1}^{k}{[{{\mu }_{i}}({{\mu }_{k+1}}-{{\mu }_{i}})]}}^{1/2}}, \\ & \frac{{{n}^{2}}{{k}^{2}}}{8(n+2)}\le {{\left( \frac{\rho \max }{\rho \min } \right)}^{2}}[\sum\limits_{i=1}^{k}{\frac{\mu _{i}^{1/2}}{{{\mu }_{k+1}}-{{\mu }_{i}}}}]\times \sum\limits_{i=1}^{k}{\mu _{i}^{1/2}}. \\ \end{align}$$