Hostname: page-component-586b7cd67f-2plfb Total loading time: 0 Render date: 2024-11-28T02:18:27.918Z Has data issue: false hasContentIssue false
  • English
  • Français

Inductive Limit Toral Automorphisms of Irrational Rotation Algebras

Published online by Cambridge University Press:  20 November 2018

P. J. Stacey
P. J. Stacey*
Affiliation:
Department of Mathematics La Trobe University Bundoora, Victoria 3083 Australia, e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Irrational rotation 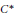${{C}^{*}}$-algebras have an inductive limit decomposition in terms of matrix algebras over the space of continuous functions on the circle and this decomposition can be chosen to be invariant under the flip automorphism. It is shown that the flip is essentially the only toral automorphism with this property.

Keywords

46L4046L35
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 44 , Issue 3 , 01 September 2001 , pp. 335 - 336
Copyright
Copyright © Canadian Mathematical Society 2001

References

[1] Boca, F. P., On the flip fixed point algebra in certain noncommutative tori. Indiana Univ. Math. J. 45 (1996), 253–273.Google Scholar
[2] Brenken, B., Representations and automorphisms of the irrational rotation algebra. Pacific J. Math. 111 (1984), 257–282.Google Scholar
[3] Elliott, G. A. and Evans, D. E., The structure of the irrational rotation C*-algebra. Ann. of Math. (2) 138 (1993), 477–501.Google Scholar
[4] Elliott, G. A. and Lin, Q., Cut-down method in the inductive limit decomposition of non-commutative tori. J. LondonMath. Soc. (2) 54 (1996), 121–134.Google Scholar
[5] Farsi, C. and Watling, N., C*-algebras of dynamical systems on the non-commutative torus. Math. Scand. 75 (1994), 101–110.Google Scholar
[6] Walters, S. G., Inductive limit automorphisms of the irrational rotation algebra. Comm. Math. Phys. 171 (1995), 365–381.Google Scholar
[7] Watatani, Y., Toral automorphisms on the irrational rotation algebras. Math. Japon. 26 (1981), 479–484.Google Scholar