Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by Crossref.
Hjorth, Greg
and
Souldatos, Ioannis A.
2009.
Independently axiomatizable ℒω1,ω theories.
The Journal of Symbolic Logic,
Vol. 74,
Issue. 4,
p.
1273.


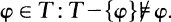 . It is countably independent if every countable subset is independent. In flnitary first order logic,
. It is countably independent if every countable subset is independent. In flnitary first order logic, 