No CrossRef data available.
Article contents
Indecomposable Higher Chow Cycles
Published online by Cambridge University Press: 20 November 2018
Abstract
Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.
Let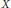 
$X$ be a projective smooth variety over a field 
$k$. In the first part we show that an indecomposable element in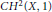 
$C{{H}^{2}}\left( X,\,1 \right)$ can be lifted to an indecomposable element in 
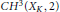$C{{H}^{3}}\left( {{X}_{K}},\,2 \right)$ where 
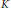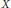$K$ is the function field of 1 variable over $k$. We also show that if $X$ is the self-product of an elliptic curve over 
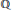$\mathbb{Q}$ then the 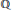$\mathbb{Q}$-vector space of indecomposable cycles 
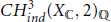$CH_{ind}^{3}{{\left( {{X}_{\mathbb{C}}},\,2 \right)}_{\mathbb{Q}}}$ is infinite dimensional.
In the second part we give a new definition of the group of indecomposable cycles of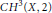 
$C{{H}^{3}}\left( X,\,2 \right)$ and give an example of non-torsion cycle in this group.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2005
References
[AMS] del Angel, P. L. and Müller-Stach, S., The transcendental part of the regulator map for K
1
on a mirror family of K3-surfaces. Duke Math. J.
112(2002), 581–598.Google Scholar
[Be] Beilinson, A. A., Higher regulators and values of L-functions. J. Soviet Math.
30(1985), 2036–2070.Google Scholar
[Be2] Beilinson, A. A., Higher regulators of modular curves. Contemp. Math.
55(1986), 1–34.Google Scholar
[Bl] Bloch, S., Lectures on algebraic cycles. Duke University Mathematics Series, IV, Duke University Mathematics Department, Durham, NC, 1980.Google Scholar
[Bl2] Bloch, S., Algebraic cycles and higher K-theory. Adv. in Math.
61(1986), 267–304.Google Scholar
[BlKa] Bloch, S. and Kato, K., L-functions and Tamagawa numbers of motives. Progr. Math.
86(1990), 333–400.Google Scholar
[DwFr] Dwyer, W. G. and Friedlander, E. M., Algebraic and étale K-theory. Trans. Amer. Math. Soc.
292(1985), 247–280.Google Scholar
[EV] Esnault, H. and Viehweg, E., Deligne-Beilinson cohomology. Perspect. Math.
4(1988), 43–91.Google Scholar
[Fl] Flach, M., A finiteness theorem for the symmetric square of an elliptic curve. Invent. Math.
109(1992), 307–327.Google Scholar
[Gi] Gillet, H., Riemann-Roch theorems for higher algebraic K-theory. Adv. in Math.
40(1981), 203–289.Google Scholar
[GL] Gordon, B. and Lewis, J., Indecomposable higher Chow cycles on products of elliptic curves. J. Algebraic Geom.
8(1999), 543–567.Google Scholar
[Ja2] Jannsen, U., Mixed motives and algebraic K-theory. Lecture Notes in Mathematics, 1400, Springer-Verlag, Berlin, 1990.Google Scholar
[Ki] Kimura, K.,
K
2 of a Fermat quotient and the value of its L-function.
K-Theory
10(1996), 73–82.Google Scholar
[MeS] Merkurjev, A. and Suslin, A. A., The group K
3
for a field.
Math. USSR Izvestija
36(1991), 541–565.Google Scholar
[Mi] Mildenhall, S., Cycles in a product of elliptic curves, and a group analogous to the class group. Duke Math. J.
67(1992), 387–406.Google Scholar
[MS] Müller-Stach, S., Algebraic cycle complexes. NATO Adv. Sci. Inst. Ser. C
548(2000), 285–305.Google Scholar
[MS2] Müller-Stach, S., Constructing indecomposable motivic cohomology classes on algebraic surfaces. J. Algebraic Geom.
6(1997), 513–543.Google Scholar
[MSC] Müller-Stach, S., Saito, S., and Collino, A., On K
1
and K
2
of algebraic surfaces. K-theory
30(2003), 37–69.Google Scholar
[Sc] Schneider, P., Einladung zur Arbeitsgemeinschaft in Oberwolfach über “Die Beilingson-Vermutung”.
Perspect. Math.
4(1988), 1–35
Google Scholar
[So1] Soulé, C., Operations on étale K-theory. Applications.
Lecture Notes in Math., 966, Springer, Boston, 1982, pp. 271–303.Google Scholar
[Sp] Spiess, M., On indecomposable elements of K
1
of a product of elliptic curves.
K-Theory
17(1999), 363–383.Google Scholar
You have
Access