Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-26T19:48:10.220Z Has data issue: false hasContentIssue false
  • English
  • Français

Hulls of Ring Extensions

Published online by Cambridge University Press:  20 November 2018

Gary F. Birkenmeier ,
Jae Keol Park  and
S. Tariq Rizvi
Gary F. Birkenmeier
Affiliation:
Department of Mathematics, University of Louisiana at Lafayette, Lafayette, LA, U.S. A. e-mail: [email protected]
Jae Keol Park
Affiliation:
Department of Mathematics, Busan National University, Busan, South Korea e-mail: [email protected]
S. Tariq Rizvi
Affiliation:
Department of Mathematics, Ohio State University, Lima, OH, U.S.A. e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

We investigate the behavior of the quasi-Baer and the right FI-extending right ring hulls under various ring extensions including group ring extensions, full and triangular matrix ring extensions, and infinite matrix ring extensions. As a consequence, we show that for semiprime rings $R$ and 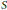$S$, if $R$ and 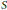$S$ are Morita equivalent, then so are the quasi-Baer right ring hulls ${{\widehat{\text{Q}}}_{\mathfrak{q}}}\mathfrak{B}(R)$ and 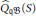${{\widehat{\text{Q}}}_{\mathfrak{q}}}\mathfrak{B}(S)$ of $R$ and 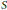$S$, respectively. As an application, we prove that if unital 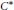${{C}^{*}}$-algebras $A$ and $B$ are Morita equivalent as rings, then the bounded central closure of $A$ and that of B are strongly Morita equivalent as 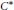${{C}^{*}}$-algebras. Our results show that the quasi-Baer property is always preserved by infinite matrix rings, unlike the Baer property. Moreover, we give an affirmative answer to an open question of Goel and Jain for the commutative group ring 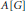$A[G]$ of a torsion-free Abelian group $G$ over a commutative semiprime quasi-continuous ring $A$. Examples that illustrate and delimit the results of this paper are provided.

Keywords

16N6016D9016S9916S5046L05(FI-) extending, Morita equivalentring of quotientsessential overring(quasi-) Baer ringring hullu.p.-monoidC*-algebra
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 53 , Issue 4 , 01 December 2010 , pp. 587 - 601
Copyright
Copyright © Canadian Mathematical Society 2010

References

[1] Ara, P. and Mathieu, M., An application of local multipliers to centralizing mappings of C*-algebras. Quart. J. Math. Oxford 44(1993), no. 174, 129–138. doi:10.1093/qmath/44.2.129Google Scholar
[2] Ara, P. and Mathieu, M., On the central Haagerup tensor product. Proc. Edinburgh Math. Soc. 37(1994), no. 1, 161–174. doi:10.1017/S0013091500018782Google Scholar
[3] Ara, P. and Mathieu, M., Local multipliers of C*-algebras. Springer Monographs in Mathematics, Springer-Verlag, London, 2003.Google Scholar
[4] Beer, W., On Morita equivalence of nuclear C*-algebras. J. Pure Appl. Algebra 26(1982), no. 3, 249–267. doi:10.1016/0022-4049(82)90109-8Google Scholar
[5] Beidar, K. and R.Wisbauer, Strongly and properly semiprime modules and rings. In: Ring Theory (Granville, OH, 1992),World Sci. Publ., River Edge, NJ, 1993, pp. 58–94.Google Scholar
[6] Birkenmeier, G. F., A generalization of FPF rings. Comm. Algebra 17(1989), no. 4, 855–884. doi:10.1080/00927878908823764Google Scholar
[7] Birkenmeier, G. F., Heatherly, H. E., Kim, J. Y. and Park, J. K. , Triangular matrix representations. J. Algebra 230(2000), no. 2, 558–595. doi:10.1006/jabr.2000.8328Google Scholar
[8] Birkenmeier, G. F., Kim, J. Y., and Park, J. K., A sheaf representation of quasi-Baer rings. J. Pure Appl. Algebra 146(2000), no. 3, 209–223. doi:10.1016/S0022-4049(99)00164-4Google Scholar
[9] Birkenmeier, G. F., Kim, J. Y., and Park, J. K., Quasi-Baer ring extensions and biregular rings. Bull. Austral. Math. Soc. 61(2000), no. 1, 39–52. doi:10.1017/S0004972700022000Google Scholar
[10] Birkenmeier, G. F., Kim, J. Y., and Park, J. K., On quasi-Baer rings. In: Algebras and Its Applications, Contemp. Math., 259, American Mathematical Society, Providence, RI, 2000, pp. 67–92.Google Scholar
[11] Birkenmeier, G. F., Kim, J. Y., and Park, J. K., Polynomial extensions of Baer and quasi-Baer rings. J. Pure Appl. Algebra 159(2001), no. 1, 25–42. doi:10.1016/S0022-4049(00)00055-4Google Scholar
[12] Birkenmeier, G. F., Müller, B. J., and Rizvi, S. T., Modules in which every fully invariant submodule is essential in a direct summand. Comm. Algebra 30(2002), no. 3, 1395–1415. doi:10.1080/00927870209342387Google Scholar
[13] Birkenmeier, G. F. and Park, J. K., Triangular matrix representations of ring extensions. J. Algebra 265(2003), no. 2, 457–477. doi:10.1016/S0021-8693(03)00155-8Google Scholar
[14] Birkenmeier, G. F., Park, J. K., and Rizvi, S. T., Modules with fully invariant submodules essential in fully invariant summands. Comm. Algebra 30(2002), no. 4, 1833–1852. doi:10.1081/AGB-120013220Google Scholar
[15] Birkenmeier, G. F., Park, J. K., and Rizvi, S. T., Generalized triangular matrix rings and the fully invariant extending property. Rocky Mountain J. Math. 32(2002), no. 4, 1299–1319. doi:10.1216/rmjm/1181070024Google Scholar
[16] Birkenmeier, G. F., Park, J. K., and Rizvi, S. T., Ring hulls and applications. J. Algebra 304(2006), no. 2, 633–665. doi:10.1016/j.jalgebra.2006.06.034Google Scholar
[17] Birkenmeier, G. F., Park, J. K., and Rizvi, S. T., The structure of rings of quotients. J. Algebra 321(2009), no. 9, 2545–2566. doi:10.1016/j.jalgebra.2009.02.013Google Scholar
[18] Birkenmeier, G. F., Park, J. K., and Rizvi, S. T., Hulls of semiprime rings with applications to C*-algebras. J. Algebra 322(2009), no. 2, 327–352. doi:10.1016/j.jalgebra.2009.03.036Google Scholar
[19] Birkenmeier, G. F., Park, J. K., and Rizvi, S. T., Modules with FI-extending hulls. Glasg. Math. J. 51(2009), no. 2, 347–357. doi:10.1017/S0017089509005023Google Scholar
[20] Camillo, V. P., Costa-Cano, F. J., and Simón, J. J., Relating properties of a ring and its ring of row and column finite matrices. J. Algebra 244(2001), no. 2, 435–449. doi:10.1006/jabr.2001.8901Google Scholar
[21] Chatters, A. W. and Hajarnavis, C. R., Rings in which every complement right ideal is a direct summand. Quart. J. Math. Oxford 28(1977), no. 109, 61–80. doi:10.1093/qmath/28.1.61Google Scholar
[22] Clark, W. E., Twisted matrix units semigroup algebras. Duke Math. J. 34(1967), 417–424. doi:10.1215/S0012-7094-67-03446-1Google Scholar
[23] Dung, N. V., Huynh, D. V., Smith, P. F., and Wisbauer, R., Extending modules. Research Notes in Mathematics Series, 313, Longman Scientofoc and Technical, Harlow, 1994.Google Scholar
[24] Elliott, G. A., Automorphisms determined by multipliers on ideals of a C*-algebra. J. Functional Analysis 23(1976), no. 1, 1–10. doi:10.1016/0022-1236(76)90054-9Google Scholar
[25] Goel, V. K. and Jain, S. K., π-injective modules and rings whose cyclics are π-injective. Comm. Algebra 6(1978), no. 1, 59–73. doi:10.1080/00927877808822233Google Scholar
[26] Jin, H. L., Doh, J., and Park, J. K., Quasi-Baer rings with essential prime radicals. Comm. Algebra 34(2006), no. 10, 3537–3541. doi:10.1080/00927870600796128Google Scholar
[27] Johnson, R. E., Structure theory of faithful rings II. Restricted rings. Trans. Amer. Math. Soc. 84(1957), 523–544. doi:10.2307/1992828Google Scholar
[28] Kaplansky, I., Rings of operators. W. A. Benjamin Inc., New York-Amsterdam, 1968.Google Scholar
[29] Lam, T. Y., Lectures on modules and rings. Graduate Texts in Mathematics, 189, Springer-Verlag, New York, 1999.Google Scholar
[30] Müller, B. J. and Rizvi, S. T., On the existence of continuous hulls. Comm. Algebra 10(1982), no. 17, 1819–1838. doi:10.1080/00927878208822805Google Scholar
[31] Pedersen, G. K., Approximating derivations on ideals of C*-algebras. Invent. Math. 45(1978), no. 3, 299–305. doi:10.1007/BF01403172Google Scholar
[32] Pollingher, A. and Zaks, A., On Baer and quasi-Baer rings. Duke Math. J. 37(1970), 127–138. doi:10.1215/S0012-7094-70-03718-XGoogle Scholar
[33] Utumi, Y., On quotient rings. Osaka Math. J. 8(1956), 1–18.Google Scholar