Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-26T22:18:40.087Z Has data issue: false hasContentIssue false
  • English
  • Français

Homology supported in Lagrangian submanifolds in mirror quintic threefolds

Part of: Symplectic geometry, contact geometry Families, fibrations Surfaces and higher-dimensional varieties

Published online by Cambridge University Press:  11 September 2020

Daniel López Garcia
Daniel López Garcia*
Affiliation:
Instituto de Matematica Pura e Aplicada (IMPA), Estrada Dona Castorina 110, Rio de Janeiro 22460-320, Brazil
*
e-mail: [email protected]
Get access Rights & Permissions [Opens in a new window]

Abstract

In this note, we study homology classes in the mirror quintic Calabi–Yau threefold that can be realized by special Lagrangian submanifolds. We have used Picard–Lefschetz theory to establish the monodromy action and to study the orbit of Lagrangian vanishing cycles. For many prime numbers 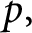$p,$ we can compute the orbit modulo p. 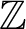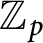We conjecture that the orbit in homology with coefficients in $\mathbb {Z}$ can be determined by these orbits with coefficients in $\mathbb {Z}_p$ .

Keywords

Lagrangian spheresmirror quintic threefoldmonodromy actionLefschetz fibrationvanishing cycles

MSC classification

Primary: 14D05: Structure of families (Picard-Lefschetz, monodromy, etc.)
Secondary: 14J30: $3$-folds 14J33: Mirror symmetry 53D05: Symplectic manifolds, general 53D12: Lagrangian submanifolds; Maslov index
Type
Article
Information
Canadian Mathematical Bulletin , Volume 64 , Issue 3 , September 2021 , pp. 709 - 724
Check for updates
Copyright
© Canadian Mathematical Society 2020

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Auroux, D., Muñoz, V., and Presas, F., Lagrangian submanifolds and Lefschetz pencils. J. Symplectic Geom. 3(2005), 171–219.Google Scholar
Auroux, D. and Smith, I., Lefschetz pencils, branched covers and symplectic invariants. In: Symplectic 4-manifolds and algebraic surfaces, Lecture Notes in Math., 1938, Springer, Berlin, 2008, pp. 1–53. http://dx.doi.org/10.1007/978-3-540-78279-7_1 CrossRefGoogle Scholar
Banyaga, A. and Hurtubise, D., Lectures on Morse homology, Kluwer Texts in Mathematical Sciences, 29, Kluwer Academic Publishers, Dordrecht, 2004. http://dx.doi.org/10.1007/978-1-4020-2696-6 Google Scholar
Brav, C. and Thomas, H., Thin monodromy in Sp(4). Compositio Math. 150(2014), 333–343. http://dx.doi.org/10.1112/S00010437X13007550 CrossRefGoogle Scholar
Candelas, P., de la Ossa, X. C., Green, P. S., and Parkes, L., A pair of Calabi–Yau manifolds as an exactly soluble superconformal theory . Nucl. Phys. B 359(1991), 21–74. http://dx.doi.org/10.1016/0550-3213(91)90292-6 CrossRefGoogle Scholar
da Silva, A. Cannas, Symplectic geometry. In: Handbook of differential geometry. Vol. II, Elsevier/North-Holland, Amsterdam, 2006. http://dx.doi.org/10.1016/S1874-5741(06)80006-3 Google Scholar
Chen, Y.-H. and Yang, Y., Monodromy of Picard-Fuchs differential equations for calabi-yau threefolds. With an appendix by Cord Erdenberger. J. Reine Angew. Math. 616(2008), 167–203. http://dx.doi.org/10.1515/CRELLE.2008.021 Google Scholar
Doran, C. and Morgan, J., Mirror symmetry and integral variations of Hodge structure underlying one parameter families of Calabi-Yau threefolds . In: Mirror symmetry, V, AMS/IP Stud. Adv. Math., 38, American Mathematical Society, Providence, RI, 2006, pp. 517–537.Google Scholar
Kontsevich, M., Homological algebra of mirror symmetry . In: Proceedings of the International Congress of Mathematicians, Vols. 1–2 (Zurich, 1994), Birkhäuser, Basel, 1995, pp. 120–139.CrossRefGoogle Scholar
Lamotke, K., The topology of complex projective varieties after S. Lefschetz. Topology 20(1981), 15–51. http://dx.doi.org/10.1016/0040-9383(81)90013-6 CrossRefGoogle Scholar
Li, T.-J. and Wu, W., Lagrangian spheres, symplectic surfaces and the symplectic mapping class group. Geom. Topol. 16(2012), 1121–1169. http://dx.doi.org/10.2140/gt.2012.16.1121 CrossRefGoogle Scholar
McDuff, D. and Dietmar, S., Introduction to symplectic topology. 3rd ed., Oxford Graduate Texts in Mathematics, Oxford University Press, Oxford, 2017. http://dx.doi.org/10.1093/oso/9780198794899.001.0001 CrossRefGoogle Scholar
Morrison, D. R., Mirror symmetry and rational curves on quintic threefolds: a guide for mathematicians. J. Amer. Math. Soc. 6(1993), 223–247. http://dx.doi.org/10.2307/21252798 CrossRefGoogle Scholar
Movasati, H. A Course in Hodge theory, with emphasis on multiple integrals. 2017. http://w3.impa.br/˜hossein/myarticles/hodgetheory.pdf.Google Scholar
Movasati, H., Gauss-Manin connection in disguise: Calabi-Yau modular forms. Surveys of Modern Mathematics, 13 (International Press, Somerville, MA), Higher Education Press, Beijing, 2017.Google Scholar
Nohara, Y. and Ueda, K., Homological mirror symmetry for the quintic 3-fold. Geom. Topol. 16(2012), 1967–2001. http://dx.doi.org/10.2140/gt.2012.16.1967 CrossRefGoogle Scholar
Schoen, R. and Wolfson, J., Minimizing area among Lagrangian surfaces: the mapping problem. J. Differ. Geom. 58(2001), 1–86.CrossRefGoogle Scholar
Seidel, P., Fukaya categories and Picard-Lefschetz theory. Zurich Lectures in Advanced Mathematics, European Mathematical Society, Zürich, 2008. http://dx.doi.org/10.4171/063 CrossRefGoogle Scholar
Thomas, R. P., An exercise in mirror symmetry . In: Proceedings of the International Congress of Mathematicians, Vol. II, Hindustan Book Agency, New Delhi, 2010, pp. 624–651.Google Scholar