Homological Dimensions of Local (Co)homology Over Commutative DG-rings

Abstract

Let $A$ be a commutative noetherian ring, let 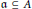$\mathfrak{a}\subseteq A$ be an ideal, and let $I$ be an injective $A$-module. A basic result in the structure theory of injective modules states that the $A$-module 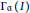${{\Gamma }_{\alpha }}\left( I \right)$ consisting of $\mathfrak{a}$-torsion elements is also an injective $A$-module. Recently, de Jong proved a dual result: If $F$ is a flat $A$-module, then the $\mathfrak{a}$-adic completion of $F$ is also a flat $A$-module. In this paper we generalize these facts to commutative noetherian 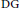$\text{DG}$-rings: let $A$ be a commutative non-positive 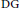$\text{DG}$-ring such that 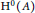${{\text{H}}^{0}}\left( A \right)$ is a noetherian ring and for each 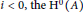$i\,<\,0,\,\text{the}\,{{\text{H}}^{0}}\left( A \right)$-module 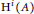${{\text{H}}^{i}}\left( A \right)$ is finitely generated. Given an ideal 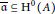$\overline{\mathfrak{a}}\,\subseteq \,{{\text{H}}^{0}}\left( A \right)$, we show that the local cohomology functor 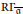$\text{R}{{\Gamma }_{\overline{\mathfrak{a}}}}$ associated with 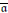$\overline{\mathfrak{a}}$ does not increase injective dimension. Dually, the derived 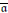$\overline{\mathfrak{a}}$-adic completion functor 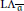$\text{L}{{\Lambda }_{\overline{\mathfrak{a}}}}$ does not increase flat dimension.