No CrossRef data available.
Article contents
Homogeneous Suslinian Continua
Published online by Cambridge University Press: 20 November 2018
Abstract
A continuumis said to be Suslinian if it does not contain uncountably many mutually exclusive non-degenerate subcontinua. Fitzpatrick and Lelek have shown that a metric Suslinian continuum 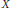 $X$ has the property that the set of points at which
$X$ has the property that the set of points at which 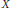 $X$ is connected im kleinen is dense in
$X$ is connected im kleinen is dense in 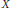 $X$. We extend their result to Hausdorff Suslinian continua and obtain a number of corollaries. In particular, we prove that a homogeneous, non-degenerate, Suslinian continuum is a simple closed curve and that each separable, non-degenerate, homogenous, Suslinian continuum is metrizable.
$X$. We extend their result to Hausdorff Suslinian continua and obtain a number of corollaries. In particular, we prove that a homogeneous, non-degenerate, Suslinian continuum is a simple closed curve and that each separable, non-degenerate, homogenous, Suslinian continuum is metrizable.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2011


