Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-25T18:01:15.868Z Has data issue: false hasContentIssue false
  • English
  • Français

Higher Moments of Fourier Coefficients of Cusp Forms

Published online by Cambridge University Press:  20 November 2018

Guangshi Lü  and
Ayyadurai Sankaranarayanan
Guangshi Lü
Affiliation:
School of Mathematics, Shandong University, Jinan, Shandong 250100, China e-mail: [email protected]
Ayyadurai Sankaranarayanan
Affiliation:
School of Mathematics, Tata Institute of Fundamental Research, Mumbai-400005, India e-mail: [email protected]
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let ${{S}_{k}}\left( \Gamma \right)$ be the space of holomorphic cusp forms of even integral weight $k$ for the full modular group 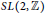$SL\left( 2,\mathbb{Z} \right)$. Let ${{\text{ }\!\!\lambda\!\!\text{ }}_{f}}\left( n \right),{{\text{ }\!\!\lambda\!\!\text{ }}_{g}}\left( n \right),{{\text{ }\!\!\lambda\!\!\text{ }}_{h}}\left( n \right)$ be the $n$-th normalized Fourier coefficients of three distinct holomorphic primitive cusp forms $f\left( z \right)\in {{S}_{{{k}_{1}}}}\left( \Gamma \right),g\left( z \right)\in {{S}_{{{k}_{2}}}}\left( \Gamma \right)$, and $h\left( z \right)\in {{S}_{{{k}_{3}}}}\left( \Gamma \right)$, respectively. In this paper we study the cancellations of sums related to arithmetic functions, such as 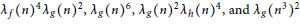$\text{ }{{\lambda }_{f}}{{\left( n \right)}^{4}}{{\lambda }_{g}}{{\left( n \right)}^{2}},\text{ }{{\lambda }_{g}}{{\left( n \right)}^{6}},\text{ }{{\lambda }_{g}}{{\left( n \right)}^{2}}{{\lambda }_{h}}{{\left( n \right)}^{4}}$, and 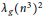${{\text{ }\!\!\lambda\!\!\text{ }}_{g}}{{\left( {{n}^{3}} \right)}^{2}}$ twisted by the arithmetic function 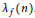${{\text{ }\!\!\lambda\!\!\text{ }}_{f}}\left( n \right)$.

Keywords

11F3011F66Fourier coefficients of automorphic formsDirichlet seriestriple product L-functionPerron’s formula
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 58 , Issue 3 , 01 September 2015 , pp. 548 - 560
Copyright
Copyright © Canadian Mathematical Society 2015

References

[1] Davenport, H., On certain exponential sums. J. Reine angew. Math. 169(1932), 158–176.Google Scholar
[2] Deligne, P., La Conjecture de Weil. Inst. Hautes Etudes Sci. Pub. Math. 43(1974), 29–39.Google Scholar
[3] Fomenko, O. M., Fourier coefficients of parabolic forms and automorphic L-functions. J. Math. Sci. (New York). 95(1999), no. 3, 2295–2316.Google Scholar
[4] Gelbart, S. and Jacquet, H., A relation between automorphic representations o/GL(2) and GL(3). Ann. Sci. École Norm. Sup. 11(1978), no. 4, 471–552.Google Scholar
[5] Good, A., The square mean ofDirichlet series associated with cusp forms. Mathematika. 29(1982), no. 2, 278–295. http://dx.doi.Org/10.1112/S0025579300012377 Google Scholar
[6] Hafner, J. L. and Me, A., On sums of Fourier coefficients of cusp forms. Enseign.Math. 35(1989), no. 3-4, 375–382.Google Scholar
[7] Hecke, E., Théorie der Eisensteinsche Reihenhoherer Stufe und ihre Anwendung auf Funktionentheorie und Arithmetik. Abh.Math.Sem. Univ. Hamburg 5(1927), no. 1, 199–224. http://dx.doi.org/10.1007/BF02952521 Google Scholar
[8] Ivic, A., On zeta-functions associated with Fourier coefficients of cusp forms. In: Proceedings of theAmalfi Conference on Analytic Number Theory (Maiori, 1989), Univ. Salerno, Salerno, 1992, pp. 231–246.Google Scholar
[9] Iwaniec, H. and Kowalski, E., Analytic number theory. American Mathematical Society Colloquium Publications, 53, American Mathematical Society, Providence, RI, 2004.Google Scholar
[10] Jacquet, H., Piatetski-Shapiro, I.I., and Shalika, J. A., Rankin-Selberg convolutions. Amer. J. Math. 105(1983), no. 2, 367–464. http://dx.doi.org/10.2307/23742 64 Google Scholar
[11] Jacquet, H. and Shalika, J. A., On Euler products and the classification of automorphic representations. I. Amer. J. Math. 103(1981), no. 3, 499–558. http://dx.doi.Org/10.2307/2374103 Google Scholar
[12] Jacquet, H. and Shalika, J. A. , On Euler products and the classification of automorphic forms. II. Amer. J. Math. 103(1981), no. 4, 777–815. http://dx.doi.org/10.2307/2374050 Google Scholar
[13] Kloosterman, H. D., AsymptotischeFormeln fur die Fourier-koeffizientenganzerModulformen. Abh.Math. Sem. Univ. Hamburg. 5(1927), no. 1, 337–352. http://dx.doi.Org/10.1 OO7/BFO295253O Google Scholar
[14] Kim, H., Functoriality for the exterior square ofGL\ and symmetric fourth ofGL2- With appendix 1 by DinakarRamakrishnan and appendix 2 by Kim and Peter Sarnak, J. Amer. Math. Soc. 16(2003), no. 1, 139–183. http://dx.doi.org/10.1090/S0894-0347-02-00410-1 Google Scholar
[15] Kim, H. and Shahidi, E., Functorial products for GL2 x GL3 and the symmetric cube for GL2 With an appendix by Colin J. Bushnell and Guy Henniart, Ann. of Math. 155(2002), no. 3, 837–893. http://dx.doi.org/10.2307/3062134 Google Scholar
[16] Kim, H. and Shahidi, E. , Cuspidality of symmetric power with applications. Duke Math. J. 112(2002), no. 1, 177–197. http://dx.doi.org/10.1215/S0012-9074-02-11215-0 Google Scholar
[17] Lau, Y.-K. and Lu, G. S., Sums of Fourier coefficients of cusp forms. Q. J. Math. 62(2011), no. 3, 687–716. http://dx.doi.Org/10.1093/qmath/haqO12 Google Scholar
[18] Lii, G. S., Average behavior of Fourier coefficients of cusp forms. Proc. Amer. Math. Soc. 137(2009), no. 6, 1961–1969.Google Scholar
[19] Lii, G. S., On sixth and eighth moments of Fourier coefficients of cusp forms. J. Number Theory. 129(2009), no. 11, 2790–2880.http://dx.doi.Org/1 0.1 01 6/j.jnt.2009.01 .01 9 Google Scholar
[20] Lii, G. S., On higher moments of Fourier coefficients of holomorphic cusp forms. Canad. J. Math. 63(2011), no. 3, 634–647. http://dx.doi.org/10.41 53/CJM-2O11-010-5 Google Scholar
[21] Lii, G. S., On higher moments of Fourier coefficients of holomorphic cusp forms. II. Montash Math. 169(2013), no. 3-4, 409–422. http://dx.doi.org/10.1007/s00605-012-0381-1 Google Scholar
[22] Moreno, C. J. and Shahidi, F., The fourth moment of the Ramanujan r-function. Math. Ann. 266(1983), no. 2, 233–239. http://dx.doi.org/10.1007/BF01458445 Google Scholar
[23] Rankin, R. A., Contributions to the theory of Ramanujan's function T(«)and similar arithemtical functions. II. The order of the Fourier coefficients of the integral modular forms. Proc. Cambridge Phil. Soc. 35(1939), 357–372.Google Scholar
[24] Rankin, R. A., Sums of cusp form coefficients. In: Automorphic forms and analytic number theory (Montreal, PQ, 1989), Univ. Montréal, Montreal, QC, 1990, pp. 115–121.Google Scholar
[25] Rudnick, Z. and Sarnak, P., Zeros of principal L-functions and random matrix theory. Duke Math. J. 81(1996), no. 2, 269–322. http://dx.doi.org/10.1215/S0012-7094-96-08115-6 Google Scholar
[26] Ramakrishnan, D. and Wang, S., A cuspidality criterion for the functorial product on GL(2) x GL(3) with a cohomological application. Int. Math. Res. Not. 2004, no. 27,1355–1394.Google Scholar
[27] Salie, H., ZurAbschatzung der FourierkoeffizientenganzerModulformen. Math. Z. 36(1933), no. 1, 263–278. http://dx.doi.org/10.1007/BF01188622 Google Scholar
[28] Selberg, A., BemerkungeniibereineDirichletscheReihe, die mit der Théorie der Modulformen naheverbundenist. Arch. Math. Naturvid. 43(1940), 47–50.Google Scholar
[29] Selberg, A., On certain L-functions. Amer. J. Math. 103(1981), no. 2, 297–355. http://dx.doi.org/10.2307/2374219 Google Scholar
[30] Selberg, A., Fourier transforms of intertwining operators and Plancherel measures for GL(«). Amer. J. Math. 106(1984), no. 1, 67–111. http://dx.doi.Org/10.2307/2374430 Google Scholar
[31] Selberg, A., Local coefficients as Artin factors for real groups. Duke Math. J. 52(1985), no. 4, 973–1007. http://dx.doi.org/10.1215/S0012-7094-85-05252-4 Google Scholar
[32] Selberg, A., A proof of Langlands’ conjecture on Plancherel measures; complementary series for p-adic groups. Ann. of Math. 132(1990), no. 2, 273–330. http://dx.doi.Org/10.2307/1 971 524 Google Scholar
[33] Walfisz, A., Ûberdie KoeffizientensummeneinigerModulformen. Math. Ann. 108(1933), no. 1, 75–90. http://dx.doi.org/10.1007/BF01452823 Google Scholar
[34] Wilton, J. R., A note on Ramanujan's arithmetical function T(«). Proc. Cambridge Philos. Soc. 25(1928), 121–129.Google Scholar
[35] Weil, A., On some exponential sums. Proc. Acad. Sci. U.S.A. 34(1948), 204–207. http://dx.doi.Org/10.1073/pnas.34.5.204 Google Scholar
[36] Wu, J., Power sums of Heche eigenvalues and application. Acta Arith. 137(2009), no. 4, 333–344. http://dx.doi.org/10.4064/aa137-4-3 Google Scholar